数据处理方法及有效数字的重要性

在量测工作中，量测结果总会有误差，这种误差与很多因素有关。因此我们在测量计算中，需要确定取几位数来代表测量或计算的结果，这就涉及有效数字问题。从计算数学的观点来说，有效数字可用来描述一个近似数的精度，一个数的相对（绝对）误差都与有效数字有关，有效数字的位数越多，相对（绝对）误差就越小。所以，在对数据的处理中，掌握有效数字的相关知识是很重要的。

（一）有效数字

有效数字的概念可表述为：由数字组成的一个数，除最末一位数字是不确切值或可疑值外，其他数字皆为可靠值或确切值，则组成该数的所有数字包括末位数字称为有效数字，除有效数字外其余数字为多余数字。

对于“0”这个数字，它在数中的位置不同，可能是有效数字，也可能是多余数字。

整数前面的“0”无意义，是多余数字。

对于纯小数，在小数点后，数字前的“0”只起定位，决定数量级的作用（相当于所取得测量单位不同），所以也是多余数字。处于数中间位置的“0”为有效数字。处于数后面位置的“0”是否算有效数字可分三种情况：

（1）若把多余数字的“0”用10的乘幂来表示，使其与有效数字分开，这样在 10 的乘幂前面所有数字包括“0”皆为有效数字。

（2）作为测量结果并注明误差值的数值，其表示的数值等于或大于误差值的所有数字，包括“0”皆为有效数字。

（3）上面两种情况外的数后面的“0”则很难判断是有效数字还是多余数字，因此应避免采用这种不确切的表示方法。

一个数中有效数字占有的位数，即有效数字的个数，为该数的有效位数。为弄清有效数字与有效位数的概念，举例如下：

有效数字

828，0.082 8，8.28，8.28×102，这 4 个数的有效位数均为 3，有效数字都是3个。再如，测量某一试件的面积，得其有效面积 A＝0.050 150 2 m2，测量的极限误差率δ＝0.000 005。则测量结果应表示为 A＝(0.050 150±0.000 005）m2。误差的有效数字为 1 位，即 5；而有效面积的有效数字应为 5 位，即 50 150；因 2 小于误差数量级，故为多余数字。

若给出的数值为 71 300，则为不确切的表示方法。它可能是 713×102，也可能是 7.13×104，也可能是 7.130 0×104。即有效数字可能是 3 位、4 位或 5 位。若无其他说明，则很难判定其有效数字究竟是几位。

在测量或计量中应取多少位有效数字，可根据下述准则判定：

（1）对不需要标明误差的数据，其有效位数应取到最末一位数字为可疑数字（也称不确切或参考数字）。

（2）对需要标明误差的数据，其有效位数应取到与误差同一数量级。

（二）数字修约

1.修约间隔

修约间隔是指确定修约保留位数的一种方式。修约间隔的数值一经确定，修约值即应为该数值的整数倍。

例如指定修约间隔为 0.1，修约值即应在 0.1 的整数倍中选取，相当于将数值修约到 1位小数。又如指定修约间隔为 100，修约值即应在 100 的整数倍中选取，相当于将数值修约到“百”数位。

0.5 单位修约（半个单位修约）是指修约间隔为指定数位的 0.5 单位，即修约到指定数位的 0.5 单位。

0.2 单位修约是指修约间隔为指定数位的 0.2 单位，即修约到指定数位的 0.2 单位。

最基本的修约间隔是 10n（n 为整数），它等同于确定修约到某数位。

2.数字修约进舍规则

我国国家标准《数值修约规则与极限数值的表示和判定》（GB/T 8170—2008），对修约方法分别做了规定。

（1）拟舍弃数字的最左一位数字小于5时，则舍去，即保留的各位数字不变。

【例 1.2.1】 将 17.447 6 修约到 1 位小数，得 17.4。

【例 1.2.2】 将 17.447 6 修约成 2 位有效位数，得 17。

（2）拟舍弃数字的最左一位数字大于 5，或者是 5，而且后面的数字并非全部是 0 时，则进 1，即保留的末位数字加 1。

【例 1.2.3】 将 1 167 修约到“百”数位，得 12×102（特定时可以写为 1 200）。

【例 1.2.4】 将 1 167 修约成 3 位有效位数，得 117×10（特定时可写为 1 170）。

【例 1.2.5】 将 10.502 修约到“个”数位，得 11。

（3）拟舍弃数字的最左一位数字为 5，而后面无数字或全部为 0 时，若被保留的末位数字为奇（1，3，5，7，9）则进1，为偶数时（2，4，6，8，0）则舍弃。

【例 1.2.6】 修约间隔为 0.1（或 10－1）。

数字修约

拟修约数值 2.050 修约值 2.0

拟修约数值 0.150 修约值 0.2

【例 1.2.7】 修约间隔为 1 000（或 103）。

拟修约数值 4 500 修约值 4×103（特定时可写为 4 000）

拟修约数值 5 500 修约值 6×103（特定时可写为 6 000）

【例 1.2.8】 将数字修约成 2 位有效位数。

拟修约数值 0.034 5 修约值 0.034

拟修约数值 34 500 修约值 34×103（特定时可写为 34 000）

（4）负数修约时，先将它的绝对值按上述三条规定进行修约，然后在修约值前面加上负号。

【例 1.2.9】 将下列数字修约至“十”数位。

拟修约数值－255 修约值－26×10（特定时可写为－260）

拟修约数值－245 修约值－24×10（特定时可写为－240）

【例 1.2.10】 将下列数字修约成 2 位有效位数。

拟修约数值－285 修约值－28×10（特定时可写为－280）

拟修约数值－0.028 5 修约值－0.028

（5）0.5 单位修约时，将拟修约数值乘以 2，按指定数位依进舍规则修约，所得数值再除以 2。

【例 1.2.11】 将下列数字修约到“个”数位的 0.5 单位（或修约间隔为 0.5）。

拟修约数值（a） 乘2 修约值（2a） 修约值（a）

50.25 100.5 100 50.0

50.38 100.76 101 50.5

－50.75 －101.5 －102 －51.0

－60.28 －120.56 －121 －60.5

（6）0.2 单位修约时，将拟修约数值乘以 5，按指定数位依进舍规则修约，所得数值再除以 5。

【例 1.2.12】 将下列数字修约到“个”数位的 0.2 单位（或修约间隔为 20）。

拟修约数值（a） 乘5 修约值（5a） 修约值（a）(www.xing528.com)

830 4 150 4 200 840

842 4 210 4 200 840

832 4 160 4 200 840

－930 －4 650 －4 600 －920

（7）拟舍去的数字并非单独的一个数字时，不得对该数值连续进行修约，应按拟舍去的数中最左面的第一位数字的大小，照上述各条一次修约完成。

如：15.454 6 修约整数，不应该 15.454 6→15.455→15.46→15.5→16 这样修约，而是15.454 6→15 这样一次修约完成。

上述数值修约规则（有时称之为“奇升偶舍法”）与以往用的“四舍五入”的方法区别在于用“四舍五入”法对数值进行修约，从很多修约后的数值中得到的均值偏大，用上述修约规则进舍的状况具有平衡性，进舍误差也具有平衡性，若干数值经过这种修约后，修约值之和变大的可能性与变小的可能性是一样的。

为便于记忆，将上述规则归纳为以下几句口诀：“四舍六入五考虑，五后非零则进一，五后为零视奇偶，奇升偶舍要注意，修约一次要到位”。

（三）可疑数据的取舍方法

在一组条件完全相同的重复试验中，个别的测量值可能会出现异常。如测量值过大或过小，这些过大或过小的测量数据是不正常的，或称为可疑的。对于这些可疑数据应该用数理统计的方法判别其真伪，并决定取舍。常用可疑数据的取舍方法有拉依达法、肖维纳特（Chauvenet）法、格拉布斯（Grubbs）法等。

1.拉依达法（3S准则）

拉依达法是美国混凝土标准所采用的方法，由于该方法以 3 倍标准差作为判断标准，所以亦称 3S 法。如果检测质量数据的总体服从正态分布 x～N（X，σ2），对于每个质量数据落在区间（－3S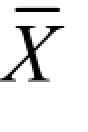，＋3S）内的概率为 99.73%，

拉依达法

而落在这个区间外面的概率仅为 0.27%，即 1 000 次测量中只可能出现 3 次。因此，在有限的测量中发生这种情况的可能性是很小，而且一旦出现，就认为该测量数据是不可靠的，应舍去。

3S 准则比较适用于样本容量 n ＞ 50 的情况。判断方法如下：

设 x1，x2，…，xn是总体中抽取的样本，其中 xi为其中过大或过小值。

（1）计算数据的平均值，如总体的标准差未知，则同时求出样本的标准差S；（2）计算，如果，则将该测量值剔除，否则保留。

另外，当测量值与平均值之差大于 2 倍标准差（）时，则该测量值应保留，但需存疑。

【例 1.2.13】 试验室内进行同配比的混凝土强度试验，其试验结果为（n＝10）：23.0 MPa，

24.5 MPa，26.0 MPa，25.0 MPa，24.8 MPa，27.0 MPa，25.5 MPa，31.0 MPa，25.4 MPa，25.8 MPa，试用拉依达法决定其取舍。

【解】 分析上述 10 个数据，xmin=23.0 MPa，xmax＝31.0 MPa 最可疑。故应首先判别 xmin、xmax，经计算：X=25.8 MPa，S＝2.10 MPa。由于

故上述测量数据均不能舍弃。

2.肖维纳特法

进行 n 次试验，其测量值服从正态分布，以概率 1/(2n) 设定一判别范围（-K nS ,K nS），当偏差（测量值xi与其算术平均值X之差）超出该范围时，就意味着该测量值xi是可疑的，应予以舍弃。判断方法如下：

（1）计算数据的平均值X，同时如总体的标准差未知，则求出样本的标准差S。

肖维纳特法

（2）对每个样本的xi值，计算，如果，则将xi剔除，否则保留。Kn为肖维纳特系数，与试验次数 n 有关，可由表 1.2.1 查得。

表1.2.1　肖维纳特系数表

【例 1.2.14】 试验结果同【例 1.2.13】，试用肖维纳特法进行判断。

【解】 查表 1.2.1，当 n＝10 时，Kn＝1.96。对于测量值 31.0 MPa，有

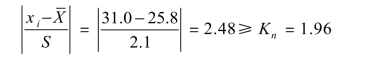
说明测量数据 31.0 是异常的，应予以舍弃。

3.格拉布斯法

格拉布斯法假定测量结果服从正态分布，根据顺序统计量来确定可疑数据的取舍。假设进行 n 次重复试验，试验结果为 x1，x2，…，xi，…，xn，而且xi服从正态分布。为了检验ix（i=1，2，…，n）中是否有可疑值，可将ix按其值由小到大的顺序重新排列，得

格拉布斯法

根据顺序统计原则，可给出标准化顺序统计量 g。

根据格拉布斯统计量的分布，在指定的显著性水平β(β=1-α，其中α为保证率，保值率是指测量数据与真实值的匹配程度或接近程度）下，求得判断可疑值的临界值g（0β, n），格拉布斯法的判断方法如下：

（1）计算数据的平均值X，同时如总体的标准差未知，则求出样本的标准差S。

（2）对每个样本的xi值，当gi≥g0(β, n)时，xi为异常值应舍弃，反之为正常值，应予以留下。其中g（0β, n）值可查表 1.2.2 得出。

表1.2.2　格拉布斯准则g0(β, n)

注：格拉布斯准则比较适用于样本容量 n≤25 的情况。

【例 1.2.15】 试用格拉布斯法判断【例 1.2.13】测量数据的真伪，显著性水平。

【解】（1）测量数据按从大到小的次序排列如下：

23.0，24.5，24.8，25.0，25.4，25.5，25.8，26.0，27.0，31.0

（2）计算数据特征量：＝25.8 MPa，S＝2.10 MPa。

（3）计算统计量：

由于g10＞g1，首先判断x10＝31.0 是否为可疑数据。

（4）根据β＝0.05，n＝10，查表 1.2.2 可得：g（00.05, 10）＝2.18。由于g10＝2.48 ＞g（00.05, 10）＝2.18，所以x10为异常值，应予以舍弃。仿照上述方法继续对余下的 9 个数据进行判别，经计算无异常值。

应用上述判断准则时应注意以下几点：

（1）剔除可疑数据时，首先应对样本观测值中的最小值和最大值进行判断，因为这两个值极有可能是可疑数据。

（2）可疑数据每次只能剔除一个，然后按剩下的样本观测值重新计算，再做第二次判断，如此逐个地剔除，直到所剩下的值不再是可疑数据为止；不允许一次同时剔除多个样本观测值。

（3）采用不同准则对可疑数据进行判断时，可能会出现不同的结论，此时要对所选用准则的适用范围，给定的检验水平的合理性，以及产生可疑数据的原因等作进一步的分析。