t分布在小样本检测分析中的应用及意义

t分布

在大样本检测分析中（如 n ＞ 50），通常认为 x 是近似地遵循正态分布。但在实际工作中，大量的工作都是进行小样本检测分析，这就要用到 t 分布以解决小样本的推断问题。在小样本检测中，由于总体标准差σ未知，若用标准差估计值S 代替σ，则统计量为t分布，记为 T～t(n)。

若 x1，x2，…，xn，n 是总体N (, σ2)的样本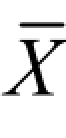，,S2分别是样本均值和样本方差，则有

根据给定的保证率 α 以及自由度 n－1，由分布概率系数表查得平均值为的单边置信区间为

1.t 分布曲线（见图 1.1.3）

t 分布曲线类似于标准正态分布，t 分布曲线有以下分布特征：

（1）t 分布曲线是一种以 0 为中心、两侧对称的类似于正态分布曲线形状的曲线。

（2）t＝0 时所对应的纵坐标为分布曲线的峰值，即纵坐标最高处。

（3）t 分布为单峰曲线，其离散程度较正态曲线大（即不如正态曲线密集）。

（4）t 分布不是一条曲线，而是随着自由度 f而变化的一簇曲线（见图 1.1.3），即随着样本所含个数（n）变化，t 分布曲线的峰值也随之变化。这种变化完全取决于计算标准差 S 的自由度（f f=n-1）；当 n 较小时，即 f ＜ 10 时，曲线低平，t 分布与正态分布曲线差别较大；当 f ＞ 100可用正态分布代替 t 分布；t→∞，t分布曲线和正态分布曲线是严格一致的，这时t=X。

图1.1.3　t 分布曲线(www.xing528.com)

2.t 分布的应用和意义

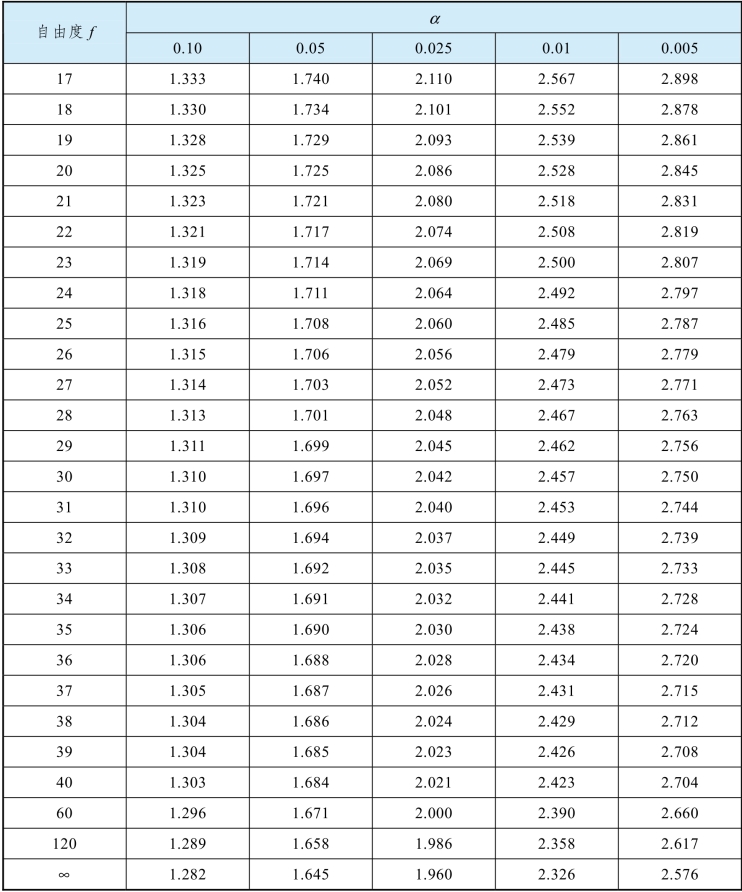
t 分布广泛应用于处理和正态分布有关的小样本检测。应用 t 分布的前提条件是两个要比较的总体方差必须具有统计上的一致性。t分布临界值表（单边）如表1.1.4 所示。

（1）比较两批产品某特征值是否有明显差异。

（2）比较一批产品是否与规格相一致。

（3）比较不同检验人员、不同检验方法或不同实验室的检验结果。

（4）检验两条回归直线的一致性。

（5）检查系统误差，估计检测结果的置信区间。

表1.1.4　t分布临界值表（单边）

续表

【例 1.1.9】 检查某路段路基压实度，共检测 30 点，得压实度平均值K＝93.5%，标准偏差 S＝3.0%，现推定其保证率为 99% 的平均值单边下置信区间。

【解】 按照单边置信区间公式有：f=n-1 =29，1-α=1 -0.99 =0.01，查 t 分布表得t1-α=t0.01=2.462。由下置信界限公式可得

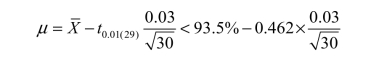
可得μ＜94.85%。这说明，平均压实度“真值”小于94.85% 的概率为99%。