
正态分布
正态分布也叫误差分布,在对某一测试对象进行多次测试时,测定值在真值附近的一定范围内波动,其中接近平均值的数值占绝大多数,大于和小于平均值的频率几乎一样,远离平均值的占少数,这种分布规律叫“正态分布”,用图形表示称为正态分布曲线。在道路检测试验中得到的数据分布规律多为正态分布。正态分布的概率密度函数计算公式为
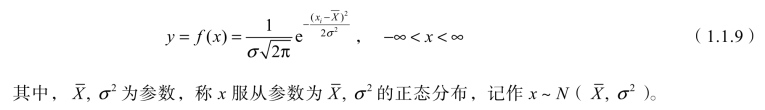
式中 y——测定值的概率密度;
X——测定值的平均值;
xi——某测定值;
σ——标准差。
f (x)的图形如图 1.1.1 所示,可以看出,正态分布曲线具有以下性质:
(1)曲线关于x=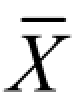 对称,表明对于任意的σ>0,有
对称,表明对于任意的σ>0,有
![]()
(2)当x=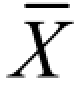 时,f(x)取到最大值,即
时,f(x)取到最大值,即
![]()

图1.1.1 正态分布图
x 离X越远,f(x)的值越小。这表明对于同样长度的区间,当区间离X越远,f(x)越小,即x落在这个区间的概率越小。
(3)在x=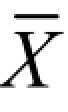 ±σ处曲线有拐点,曲线以 x 轴为渐近线。
±σ处曲线有拐点,曲线以 x 轴为渐近线。
(4)若令![]() ,并将其代入式(1.1.9)中,则得
,并将其代入式(1.1.9)中,则得
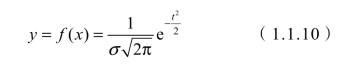
特别指出,当 =0, σ=1时,此时的正态分布称为标准正态分布,记为N(0, 1)。其标准正态分布图形如图 1.1.2所示,整个正态分布曲线与横轴之间所包含的总面积(即概率)应为 1,其分布函数为
=0, σ=1时,此时的正态分布称为标准正态分布,记为N(0, 1)。其标准正态分布图形如图 1.1.2所示,整个正态分布曲线与横轴之间所包含的总面积(即概率)应为 1,其分布函数为
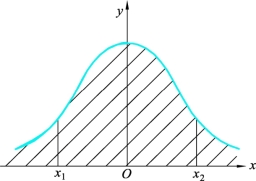
图1.1.2 标准正态分布图


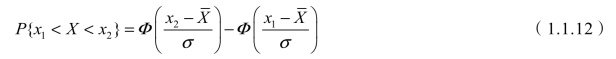
表1.1.1 标准正态分布概率系数表(https://www.xing528.com)
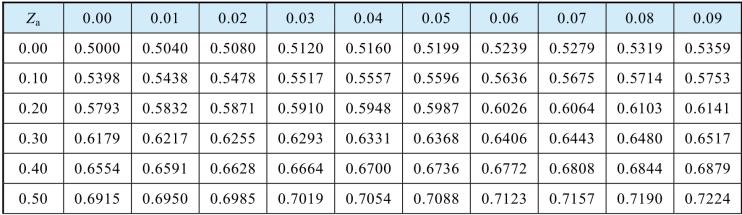
续表
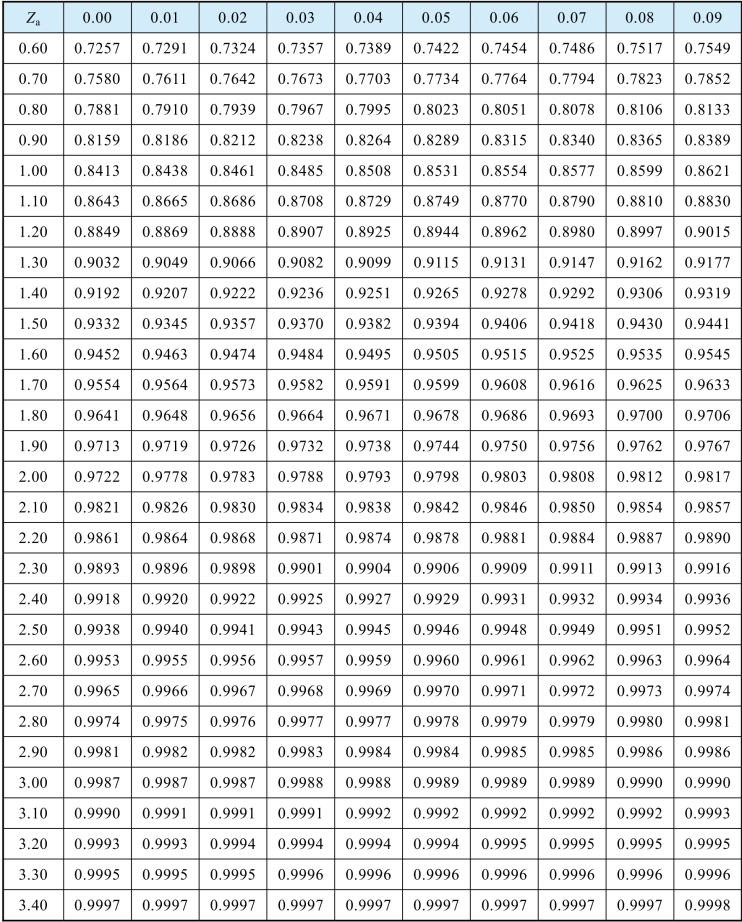
表1.1.2 路基路面检测常用系数表

【例 1.1.7】 若某检测值 x~N(0, 1),求 P{-1 < x < 1}。
【解】 由于该检测值服从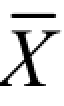 =0, σ=1的正态分布,则有
=0, σ=1的正态分布,则有

查表1.1.1,当 Za=1 时,Φ(1)=0.8413,P{-1 < x < 1}=2Φ(1)-1,则有
P{-1 < x < 1}=68.26%
利用公式(1.1.12),我们可以求得双边置信区间的几个重要数据:

式中,Za通常称为保证率系数,在工程应用中,其取值与公路的等级有关。X为样本平均值,σ常用样本标准差 S 代替。式(1.1.13)可以这样理解:试验所测得的值在误差区间( -Zaσ,X+Zaσ)的可能性(或概率值)的大小,如 P{
-Zaσ,X+Zaσ)的可能性(或概率值)的大小,如 P{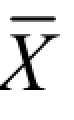 -3σ < x <
-3σ < x <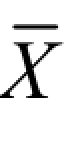 +3σ }=99.73%,理解为:试验所测得的值在误差区间(
+3σ }=99.73%,理解为:试验所测得的值在误差区间(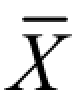 -3σ,
-3σ,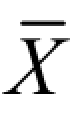 +3σ)的概率为 99.73%。在工程试验中,我们所测得的实际值是很难达到这个精度要求的。但我们可以人为地制定误差区间,即规定 Za值的大小,或规定合格率的大小。如果检测值满足规定的要求,则数据合格;否则,数据不合格。
+3σ)的概率为 99.73%。在工程试验中,我们所测得的实际值是很难达到这个精度要求的。但我们可以人为地制定误差区间,即规定 Za值的大小,或规定合格率的大小。如果检测值满足规定的要求,则数据合格;否则,数据不合格。
【例 1.1.8】 某预应力混凝土梁设计强度 RD=40 MPa,按规定的方法制备试块,经 28 d标准条件养护后,各组试块抗压强度如表 1.1.3 所示,规范要求合格率为 85%,求该批混凝土平均值、标准差、变异系数,并对该批混凝土进行质量评定,(混凝土立方体抗压强度标准值计算公式为: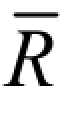 =RD+Zaσ)。
=RD+Zaσ)。
表1.1.3 混凝土强度试验结果

【解】 根据公式有


抗压强度标准值计算公式:

查表 1.1.1 可得 Φ(1.09)=0.862 1,Φ(1.10)=0.864 3。
内插可得:
P=Φ(1.097)=0.862 1+(0.864 3-0.862 1)×0.7=86.36% > 85%
故该批混凝土质量合格。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




