道路工程试验与检测数据统计特征

检测数据的统计特征数

检测数据常用的统计特征数可分为位置特征数和离散特征数两类。位置特征数是分析计量数据的基本指标。通常，我们所获得的检测数据是分散的，必须通过平均数把它们集中起来，反映其共同趋向的平均水平，它表达了数据的集中位置。位置特征数一般包括算术平均值、中位数等。离散特征数表示数据离散性质或波动程度，表达随机变量的各变值大小的差异程度。常用的离散特征数有极差、标准偏差、变异系数等。

（一）位置特征数

1.算术平均值

算术平均值是表示一组数据集中位置最有用的统计特征数，经常用样本的算术平均值来代表总体的平均水平。总体的算术平均值用 μ 表示，样本的算术平均值用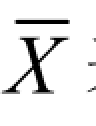表示。如果n个样本数据为x1，x2，…，xn，那么样本的算术平均值为

【例 1.1.2】 某路段沥青混凝土面层进行抗滑性能检测时，其摩擦系数BF的检测值（共 10点）分别为 54，52，60，58，47，55，60，62，63，54（摆值），求摩擦系数的算术平均值。

【解】 根据算术平均值计算公式，该路面摩擦系数算术平均值为

2.中位数

在一组数据 x1，x2，…，xn中，按其大小次序排序，以排在正中间的一个数表示总体的平均水平，称之为中位数，或称中值，用Dm表示。n 为奇数时，正中间的数为中位数；n为偶数时，正中间的数有2个，则取这2个数的平均值作为中位数，即

【例 1.1.3】 检测值同【例 1.1.2】，求中位数。

【解】 检测值按大小次序排列为：63，62，60，60，58，55，54，54，52，47（摆值），则中位数为

（二）离散特征数

1.极 差

极差又称全距，指在一批数据中最大值与最小值相减之差。常用于测定数值的离散程度，适合于小样本，可以了解产品的波动范围和波动程度，但容易受样本中异常值的影响，不能表示内部频数的分布情况。

【例1.1.4】 检测值同【例 1.1.2】，计算数据的极差。

【解】 根据公式（1.1.5），检测数据的极差为(www.xing528.com)

在生产中，只反映产品的平均水平是不够的，如混凝土强度太高或太低都不好。即使平均值符合要求，但当数值波动太大时，产品质量也不能让人满意。因此需要了解数据波动范围的大小。极差没有充分利用数据的信息，但计算十分简单，仅适用于样本容量较小（n＜10）的情况。

2.标准偏差

标准偏差用 S 表示，又称标准差或均方差，指每次测定值与平均值的均方根值，是描述检测数据离散程度的最重要指标。它与平均值结合起来就能更全面地说明一批检测变量值的分布情况，可以用来评定相同等级材料的质量。S 愈小表示测定值离散程度小，S 愈大表示离散程度大。其计算公式为

（1）总体的标准差：

（2）样本的标准差：

在质量检验中，总体的标准差 S 不易求得，一般我们计算样本的标准偏差来衡量数据的分散程度以及波动性。

【例 1.1.5】 检测值同【例 1.1.2】，求样本标准偏差 S。

【解】 根据公式（1.1.7），样本标准偏差为：

3.变异系数

标准偏差可反映样本数据的绝对波动状况，当测量较大量值时，绝对误差一般较大；测量较小量时，绝对误差一般较小。而变异系数反映的是数据相对波动的状况，变异系数用 Cv表示，指一组测定值的标准差和其算术平均值之比，是衡量一批数据中各个检测值的相对离散程度，表明重复测定结果的变异程度，可以用来比较平均值不同的几组材料变量值的变异情况。Cv值愈小表示测定值离散程度小，Cv愈大表示离散程度大。其计算公式为

【例 1.1.6】 若甲路段沥青混凝土面层的摩擦系数算术平均值为 55.2（摆值），标准偏差为4.13（摆值）；乙路段的摩擦系数算术平均值为 60.8（摆值），标准偏差为4.27（摆值）。试计算两路段的变异系数。

【解】 根据公式（1.1.8），两路段的变异系数分别为

甲路段变异系数 Cv＝4.13/55.2×100%＝7.48%

乙路段变异系数 Cv＝4.27/60.8×100%＝7.02%

从标准偏差看，甲路段标准偏差小于乙路段标准偏差。但从变异系数分析，甲路段变异系数大于乙路段变异系数，说明甲路段的摩擦系数相对波动比乙路段的大，面层抗滑稳定性比乙差。