考生要彻底地解决排列组合概率问题:第一,要掌握基本原理;第二,要掌握本部分的模型;第三,对模型对应的例题勤加练习.
技巧攻略(一) “相邻问题”——捆绑法
将必须相邻的元素捆绑在一起作为一个整体,连同剩下的元素再全排列,这种方法叫作捆绑法.
例如,甲、乙等10名同学排成一列,要求甲、乙相邻,那么有多少种不同的排列方法?

技巧攻略(二) “不相邻问题”——插空法
将不能相邻的元素放到一边暂不考虑,先把剩下的元素全排列,这些全排列的元素之间形成了许多间隔,此时便可以将不能相邻的元素排到这些间隔中去,这种方法叫作插空法.
例如,甲、乙等10名同学排成一列,要求甲、乙不相邻,那么有多少种不同的排列方法?

技巧攻略(三) “同元分配问题”——挡板法
挡板法专门解决元素相同的分配问题.将相同元素分配给不同对象时,先将元素一字摆开,然后从间隔中选出所需的个数,插入挡板,将元素分成若干段,这种分配方法叫作挡板法.挡板法得到的每个对象都至少有一个元素.
例如,把10瓶相同的饮料分给3个人,每个人至少分得1瓶,有多少种不同的分法?
将10瓶饮料一字摆开,形成9个间隔,要分成3段,只需要从9个间隔中取出2个插入挡板即可.故不同的分法总数为![]()
技巧攻略(四) “不同元分配问题”——打包寄送法
打包法专门解决元素不同的分组问题.将不同元素分组时,先将元素个数进行正整数分解并利用排列组合计算每一种分解所对应的不同分组情况,然后汇总相加,这种分组方法叫作打包法.打包法得到的每一组都至少有一个元素.
例如,6名教师分成3个小组,有多少种不同的分组方法?(https://www.xing528.com)
解:首先,6=1+1+4=1+2+3=2+2+2,则6共有三种分解方法.其次,求出每种分解所对应的分组方法数,
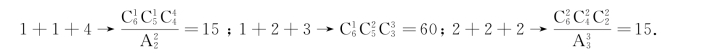
汇总相加可得15+60+15=90种不同的分组方法.
寄送法实际上就是将n个不同的元素分到n个不同的位置,每个位置恰好一个元素,不同的寄送方法为全排列Ann.打包法与寄送法结合在一块就是打包寄送法.
例如,6名教师分配到3个边疆地区支教,每个地区至少去一名教师,有多少种不同的分配方法?
分两步:第一步,打包(分组),共有90种方法;第二步,寄送,共有6种方法.根据乘法原理可得,不同的分配方法有90×6=540种.
技巧攻略(五) “各不归位问题”——错排法

技巧攻略(六) “正难则反问题”——间接法
对于没有、全部、至少、至多型的概率问题常常采用正难则反法,即先考虑对立事件的概率,然后用1减去这个概率.
例如,一箱产品共有100个,其中次品有5个,验货时从箱子中随机抽取3件进行检验,规定抽检的产品全部为正品时才可以收货,那么验货方拒绝收货的概率p为多少?
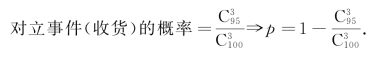
技巧攻略(七) 抽签原理:签无差别,取出不放回,则每人中奖概率相同

技巧攻略(八) 对立取反法
对于没有、全部、至少、至多型的概率问题常常采用对立求反的方法,即先考虑对立事件的概率,然后用1减去这个概率.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




