（1）锐角：若0＜∠A＜90°，则称∠A为锐角.
直角：若∠A＝90°，则称∠A为直角.
钝角：若90°＜∠A＜180°，则称∠A为钝角.
平角：若∠A＝180°，则称∠A为平角.
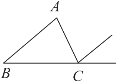
三角形内角和证明思路图
余角：若∠A＋∠B＝90°，则称∠A与∠B互为余角.
补角：若∠A＋∠B＝180°，则称∠A与∠B互为补角.
（2）对顶角：∠1与∠3，∠4与∠5.对顶角相等.
邻补角：∠1与∠2，∠2与∠3.邻补角互补.
（3）内错角：∠3与∠4.两线平行⇔内错角相等.
同位角：∠1与∠4，∠3与∠5.两线平行⇔同位角相等.
同旁内角：∠2与∠4.两线平行⇔同旁内角互补.
（4）内角和：一个凸多边形所有内角之和.
三角形内角和为180°.
四边形的内角和为360°.
凸n边形内角和为180°（n－2）.
多边形内角和证明思路图
(www.xing528.com)
外角和：三角形、四边形、凸n边形的外角和都为360°.
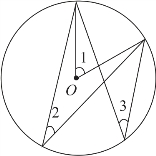
（5）圆周角：顶点在圆周上，角的两边是圆的两条弦，这样的角叫作圆周角.
同弧或等弧所对的圆周角相等.（∠3＝∠2）
圆心角：以圆心为顶点，两条半径为两边的角叫作圆心角.（∠1）
同弧或等弧所对的圆心角相等.
同弧或等弧所对的圆心角是所对圆周角的两倍.（∠1＝2∠2＝2∠3）
例1 如图2－7－1所示，在圆O内，已知∠ACB＝20°，则∠OAB＝（ ）.
A.50° B.55° C.60° D.65° E.70°
解析 由圆心角、圆周角性质可得：
∠AOB＝2∠ACB＝40°.
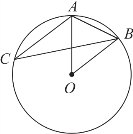
图2－7－1
综上所述，答案是E.例2 如图2－7－2所示，在△ABC中，AB∥DE，DC＝DE，且∠α＝45°，则∠β＝（ ）.
A.45° B.60° C.67.5° D.112.5° E.135°解析 因为AB∥DE，所以∠BAC＝∠EDC＝∠α，
∠ABC＝∠DEC＝∠β.
又因为DC＝DE，所以∠DEC＝∠ECD＝∠β.
在△EDC中，∠α＋2∠β＝180°⇒∠β＝67.5°.
综上所述，答案是C.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
