(1)直线方程的5种形式
1)点斜式:y-y0=k(x-x0).
【适用】已知点P(x0,y0)和斜率k.
【局限】不能表示垂直于x轴的直线.
2)斜截式:y=kx+b.
【适用】已知斜率k和直线在y轴上截距b.
【局限】不能表示垂直于x轴的直线.
![]()
【适用】已知直线上两点P1(x1,y1),P2(x2,y2).
【局限】不能表示垂直于x轴的直线.
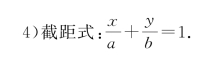
【适用】已知x轴上的截距为a,y轴上的截距为b.
【局限】不能表示通过原点或垂直于坐标轴的直线.
5)一般式:Ax+By+C=0(A2+B2≠0).
例2 (条件充分性判断)过A,B两点的直线方程为y-x+5=0.
(1)点A(3,-2),点B(5,0).

则直线方程为y-0=1×(x-5),
即y-x+5=0,可推出结论.

则直线方程为y-1=1×(x-6),
即y-x+5=0,可推出结论.(https://www.xing528.com)
综上所述,答案是D.
例3 直线ax+by+c=0通过第一、二、三象限,则( ).
A.ab>0,bc<0 B.a=0,bc<0 C.ac>0,bc<0
D.c=0,ab>0 E.以上结果均不正确

综上所述,答案是C.

图2-6-2
(2)圆方程
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫作圆(第一定义);平面内到定点的距离等于定长的点的集合(第二定义).
圆的方程如下:
1)标准式:(x-x0)2+(y-y0)2=r2 【圆心O(x0,y0)和半径r】.
2)一般式:x2+y2+Dx+Ey+F=0 【D2+E2-4F>0】.
例4 (条件充分性判断)以线段AB为直径的圆的方程是x2+y2-8x-16y+78=0.(1)点A(3,9). (2)点B(5,7).
解析 条件(1)和(2)单独不能推出结论,联合能推出结论.推导:
设圆为(x-x0)2+(y-y0)2=r2.

综上所述,答案是C.
【点评】考生可以进一步学习:圆的方程还有第三种形式(可以作为结论):
直径式:(x-x1)(x-x2)+(y-y1)(y-y2)=0【直径端点为A(x1,y1),B(x2,y2)】
应用:本题中圆的方程是(x-3)(x-5)+(y-9)(y-7)=0,展开即得结论.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




