绝对值的定义、几何意义和性质

（1）定义：正数的绝对值是它本身，负数的绝对值是它的相反数，零的绝对值为零.

（2）几何意义：数轴上的点到原点的距离叫作这个数的绝对值，两个数之差的绝对值表示数轴上这两个数相对应的点之间的距离.

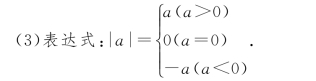
（4）性质：

对称性：|－a|＝|a|，即互为相反数的两个数的绝对值相等.

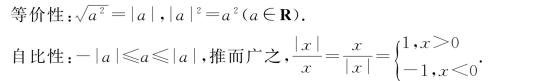
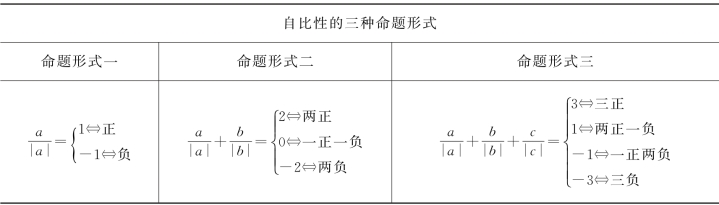
非负性：即|a|≥0，任何实数a的绝对值非负.

（5）数轴：实数与数轴上的点一一对应.数轴是有原点、刻度和方向的直线.方向指数轴的正向，一根水平的数轴正向一般指向右方，原点对应的实数为0，正数在原点的右侧，数越大在数轴上对应的点就越靠右.

例1　（条件充分性判断）|y－x|＋|z－y|－|z|＝x.

（1）x，y，z在数轴上的位置如图2－2－1所示：

图2－2－1

（2）x，y，z在数轴上的位置如图2－2－2所示：

(www.xing528.com)

图2－2－2

解析　条件（1）能推出结论，条件（2）推不出结论.推导：

（1）x，y，z在数轴上的位置如图2－2－1所示：

|y－x|＋|z－y|－|z|＝－（y－x）－（z－y）＋z＝x，能推出结论.

（2）x，y，z在数轴上的位置如图2－2－2所示：

|y－x|＋|z－y|－|z|＝（y－x）＋（z－y）－z＝－x，不能推出结论.

综上所述，答案是A.

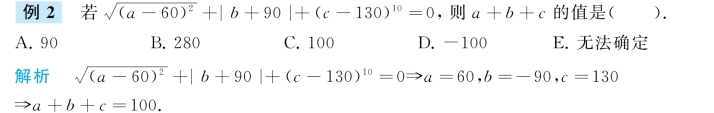
综上所述，答案是C.

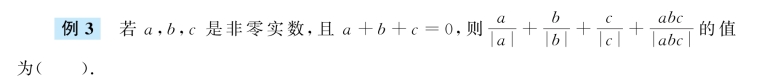
A.0　B.1或－10　C.2或－20　D.0或－20　E.3

若a，b，c两正一负，不妨设a＞0，b＞0，c＜0，则原式＝1＋1－1－1＝0.

若a，b，c一正两负，不妨设a＞0，b＜0，c＜0，则原式＝1－1－1＋1＝0.

综上所述，答案是A.