内摆式乘客门的结构与设计-案例分享

内摆式乘客门主要应用在公交车型上，这是由公交车的使用工况即乘车高峰期客流的拥挤程度和内摆式结构门的开度决定的。

同外摆式乘客门一样，内摆式也有单内摆和双内摆两种型式，它们的机构原理是一样的，我们首先讲解单内摆式乘客门。

目前大量使用的单内摆门，按其弯臂的型式特点可分为两种类型：外弯臂型和内弯臂型。

外弯臂型：弯臂外露，从车外可见；内弯臂型：弯臂内藏，车外不可见。

图5-54所示是一款外弯臂型单内摆乘客门的结构图，其机构原理可表述如下：

门体与上下弯臂铰接连接，当转轴与弯臂在门泵的驱动下转动时，门体与弯臂的上下铰接点是确定的，但门体的空间姿态不是唯一的，它可围绕上下铰接点转动。我们知道，必须有三个不共线的点才能唯一确定刚体的空间位置，那么此时对于内摆门而言，这第三点就是固定于门体上的平衡臂，由于其上的滚轮被约束，它只能在固定位置的滑道上运动。因此，门体内摆的运动过程就被确定了。

1.内摆式乘客门的结构

外弯臂型单内摆乘客门如图5-54所示，其主要结构解释如下：

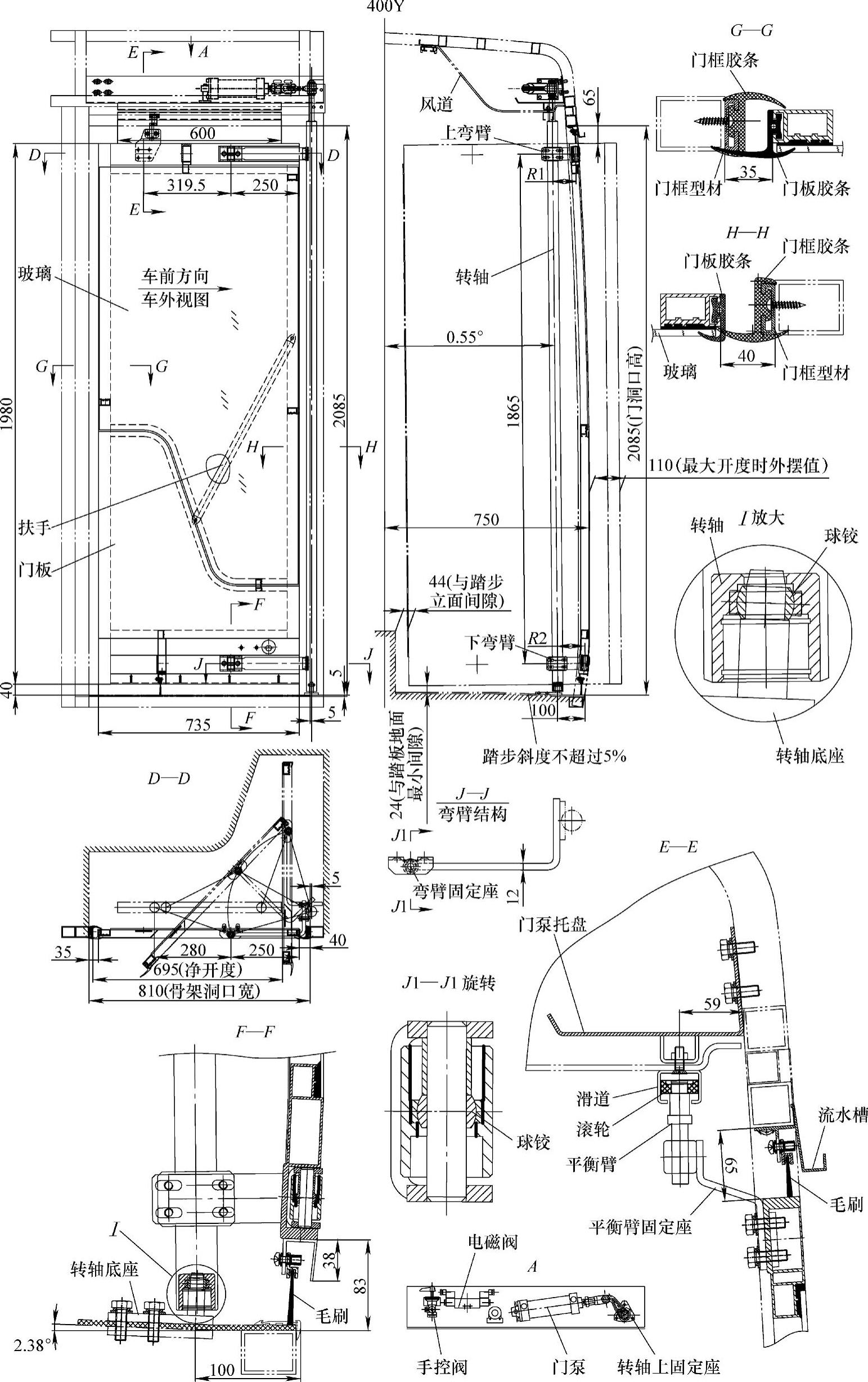
图5-54 外弯臂型单内摆乘客门

①门泵：气动泵，门体开关的动力来源。

②转轴：Φ38mm钢管喷塑，门体运动学分析的回转中心。

③弯臂：上下各一件，由12mm厚钢板制成，其必须有足够的刚度以保证门体的运动稳定性。弯臂与门体通过弯臂固定座连接，弯臂与固定座之间的铰链一般是设计成球头铰链的，这是因为门体都是带弧度的，而且这种弧度还不太可能是对称的，因此为了门体的回转自如，球铰的设计是必要的。如图5-54所示，上弯臂铰接点距转轴的回转半径R₁=84mm，下弯臂铰接点距转轴的回转半径R₂=100mm，门体的上下铰接点实际是在锥面上作回转运动，而且为了减小这种锥度，转轴的上固定点人为地内倾，使转轴同铅垂线（400Y线）形成夹角0.55°。

另外，由于结构上的限制，上下弯臂尽可能地布置于门体的上下两端，这是为了能效地利用门体骨架型材为弯臂安装所预留的结构空间。

④平衡臂：由固定座、平衡臂和滚轮等组成，刚性地固定于门体之上，滚轮被约束只能沿滑道运动。

⑤滑道：门体姿态的约束线，设计槽深时应注意校核门体沿锥面母线摆动时滚轮的上下位移量。

⑥转轴底座：由于受公交车一级踏步的限制，因此转轴底座同转轴的连接也设计成球铰型的。一级踏步面通常设计成斜面，坡度一般不大于5%（相当于2.9°），如图中的2.38°。

⑦门体：图5-54中所示是铝合金的，也可以采用钢结构。

⑧玻璃：钢化玻璃，厚5mm。

⑨扶手：上车扶手，钢管喷塑或不锈钢，规格Φ32mm。

⑩门框型材：铝型材，固定门框胶条用的。

⑪ᣘᣢ门框胶条：密封胶条，三元乙丙材料。

⑪ᣘ⑫门板胶条：密封胶条，三元乙丙材料，两种断面，前后不一样。

⑪ᣘ⑬毛刷：上下门边的挡水件。实际上由于公交车车速低、门开关频繁，对车门的密封要求已不是很严格了。毛刷只是起到挡水作用，目前还没有太好的办法来解决内摆式乘客门的密封问题。

2.单内摆门结构参数的求法

（1）求弯臂同门体铰接点的位置 如图5-55所示，我们对图5-54做如下简化：门体视为平板mn、门体与门框骨架两个表面在同一平面上、上下弯臂的回转半径相等、略去胶条，那么图5-54的空间摆动就简化成图5-55的平面摆动，且门的最大开度位置m′n′与mn垂直。

对于图5-55中未知量X，在Rt△AQO中，由勾股定理得：

R²=（W+e-a-X）2+h²

同样，在Rt△A′PO中，由勾股定理得：

R²=（X-d-h）2+（B+e）2

由以上两式得：

X=〔（W+e-a+d+h）-（B+e+h）（B+e-h）/（W+e-a-d-h）〕/2；

可直观地看出如下结论：

①X的值与b值无关。

②（B+e+h）（B+e-h）/（W+e-a-d-h）此项的值会很小，如取W=850mm，B=100mm，e=5mm，h=110mm，a=35mm，d=100mm，则算得其值为-1.76mm，由此可认为X≈（W+e-a+d+h）/2。(www.xing528.com)

③实际上X的位置是门体中心靠近转轴一点的位置。

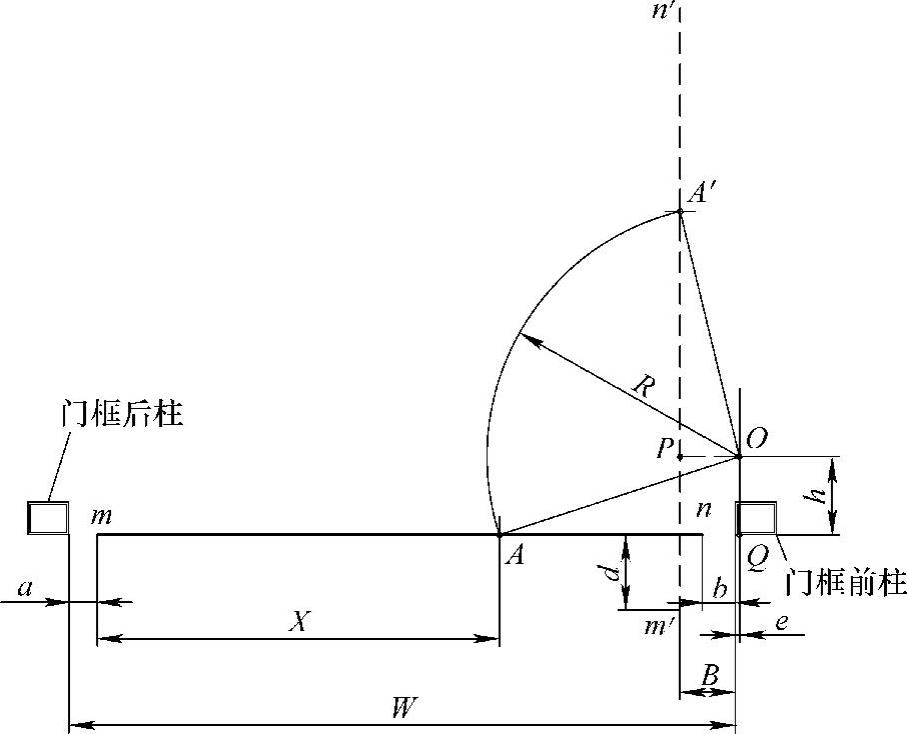
图5-55 单内摆门弯臂半径的确定

mn—门体的起始位置 m′n′—门体的最终位置 A—门体在起始位置时的弯臂铰接点 A′—门体在最终位置时的弯臂铰接点 O—动力机构的转轴中心 P—OP⊥m′n′之点 Q—OQ⊥mn之点 R—弯臂的回转半径 W—门框的骨架洞口宽度，对于单内摆门，W=750～850mm X—弯臂铰接点在门体上的位置，此值未知待求 B—在门体最大开度时门体与门框骨架的间隙， B=门体外表面在上下铰接点之间的弧高（约10～20mm）+预留间隙（约60～80mm） a—门体与门框后柱之间的间隙，不含胶条。在图5-54的结构中，

a=35mm b—门体与门框前柱之间的间隙，不含胶条。在图5-54的结构中，b=40mm d—在门体最大开度时门体超出车身表面的尺寸，此值也叫外摆值，一般地，取d=80～140mm e—转轴中心相对于门框前柱的前后位置，由于安装空间的限制，一般地，取e=0～10mm h—转轴中心相对于车身的左右位置，实际上此值是上下弯臂半径在YOZ平面上投影值R₁和R₂的平均值。一般地，取h=100～120mm.。由于安装空间的限制，转轴不可能离车身外表面太远

（2）求平衡臂的位置 实际就是求滑道的位置。如图5-56a所示，按惯用的方式，滑道是平行于门板的。因此假设滑道所在的直线uv距门板mn的距离为H，那么在门体开度最大位置m′n′时，uv在u′v′处。因此，uv与u′v′的交点B′就是平衡臂滚轮的位置，反推到门的初始位置，B点就是平衡臂滚轮的初始位置。从几何上讲，B′点永远在直线mn和直线m′n′夹角的角平分线上。

AB长度的解析表达式如下：

AB=A′B′=〔H²+（X-d-H）²〕^1/2=〔2H²-2（X-d）H+（X-d）²〕^1/2

当H=（X-d）/2时，AB取最小值，AB_min=2^-1/2（X-d）

从几何上来讲，AB的最小值是A′点到直线mn和直线m′n′交角的角平分线ST上的垂直距离A′B″，如图5-57所示。但此时H=（X-d）/2的值很大，已没有实际的工程价值。

另一个极端的情况是，平衡臂的滚轮在A点的正上方，即AB⊥mn。那么假设AB⊥mn成立，则在图5-57中，必有AS=A′S，

即X-d=W-X-B

X=（W+d-B）/2

而我们已求得X≈（W+e-a+d+h）/2，所以可得到下式：

a=e+B+h

从工程意义上讲，上式不可能成立，所以我们说平衡臂的滚轮不能在A点的正上方，只能在A点的后面。

按道理H值可有无穷多个，就是说滑道的位置可有多种选择。但由于实际安装空间的限制，H可选择的范围并不大。从稳定性的角度考虑，H值越大，平衡臂的刚度越难保证。因此，H值应尽可能取最小值，即滑道的安装位置要尽可能靠近侧围，此时由图5-56中可看出A、B两点间距也会增大，这样也对门体摆动的平衡性有好处。

平行滑道的求法是一种逆向算法，我们也可采用正向算法，如图5-56b所示，在门的初始位置给定了平衡臂滚轮的位置B点，当门体在最大开度位置m′n′时，滚轮在B′点，此时B与B′点所在的直线uv就不平行于门的初始位置mn。更广义地讲，过B和B′的任意曲线都可作为滑道线，如图中的圆弧线和S形状曲线，但这会给制造和装配带来困难，因此不具有应用价值。

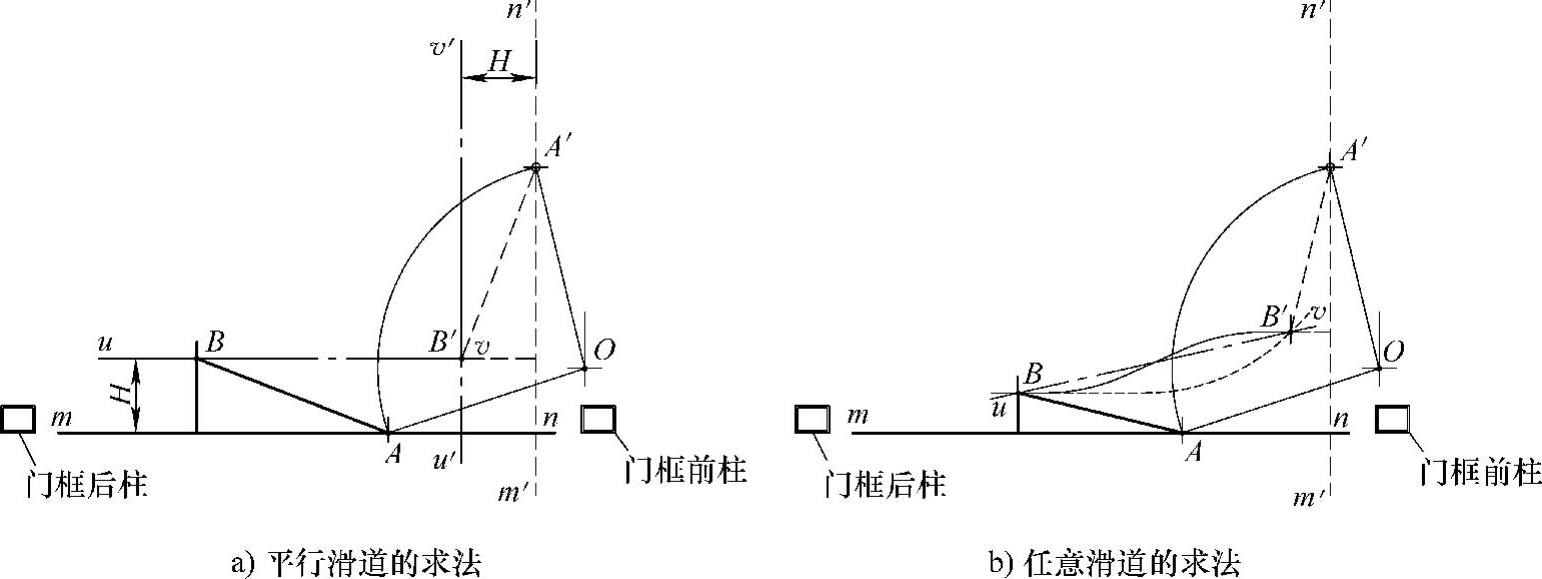
图5-56 单内摆门平衡臂滑道的确定

以上只是理想化地求得了内摆式乘客门的主要参数，有了这种初步结果后，还要回到具体结构中去校核每一个细节问题，比如门板的弧度、厚度等对计算结果的影响。从上面的分析计算过程还可看出，为了门体的计算方便，公交车的侧曲线也应设计得越平直越好。

还需作出门体的轨迹图，以校核踏步的位置。此种校核只需几何作图法即可，无需用解析法，如图5-58所示，踏步与门体运动轨迹包络线的间隙至少应保持50mm。

在了解了外弯臂型内摆式乘客门后，我们很容易将其推广到双内摆的情况：所有的结构和运动原理都同单内摆式一样，只是双门在中间的密封胶条是不一样的，如图5-59所示。

下面简单讲讲内弯臂型内摆门，其运动机构的算法同上面讲的外弯臂型是一样的，不再多说。二者主要区别在弯臂型式上：内弯臂从车外是见不到的，它与门体的铰接点布置在车内。此时可带来两点变化：一是上下铰接点的连线可设计成与转轴平行，二是弯臂是直杆型的，视需要也可是弯杆型的，如图5-60所示，此种结构优点有两个：①机构刚度好；②门净开度增大。

此种结构的缺点是密封不好，门的每一次开关其下边的毛刷都要与弯臂刮擦一次。因而，门体下边的密封毛刷或塑胶挡板也设计成了可翻转摆动的结构。

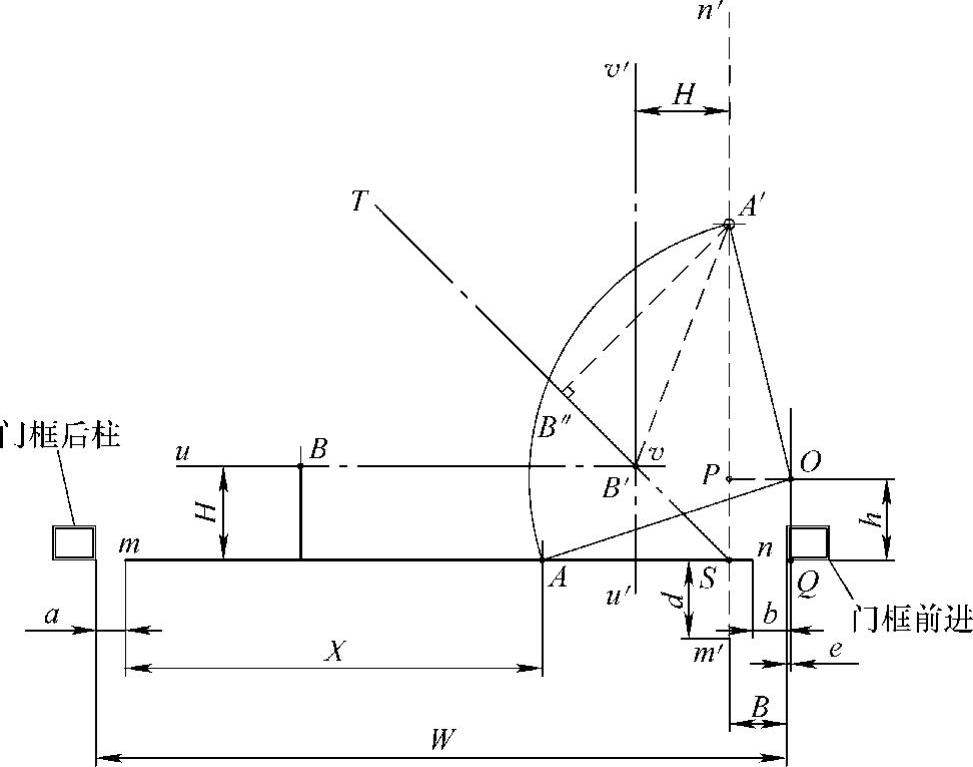
图5-57 单内摆机构数学解的几何意义

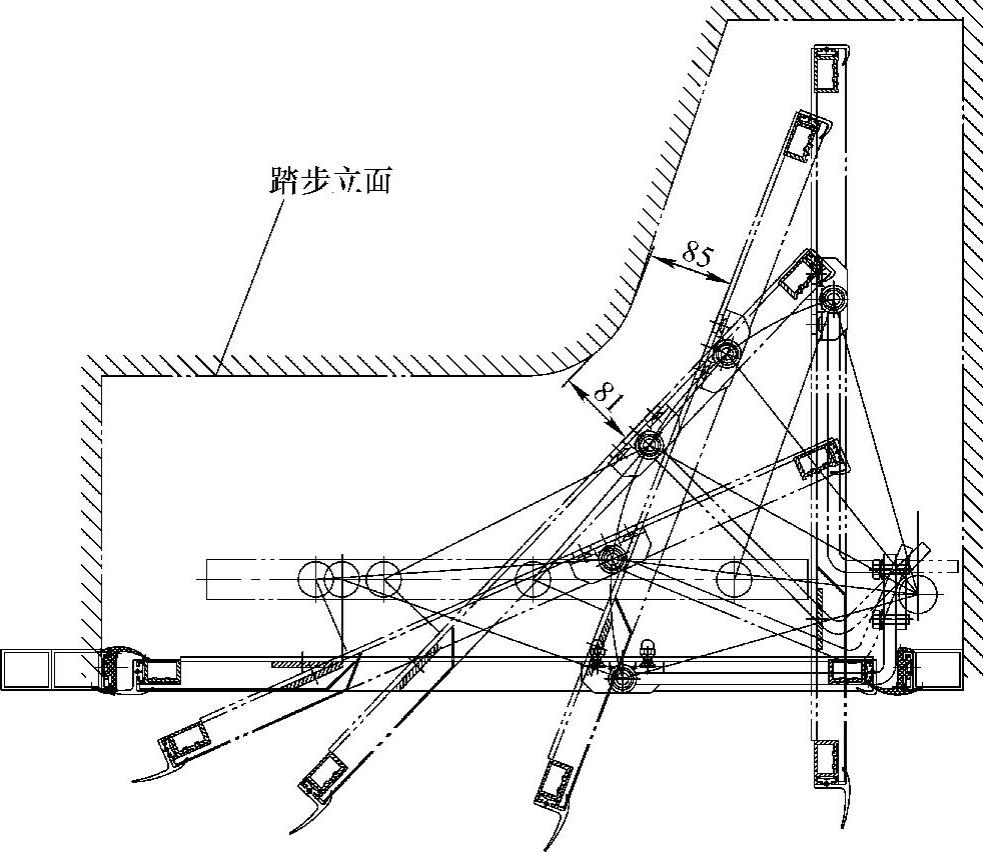
图5-58 踏步与门体运动轨迹包络线的间隙校核

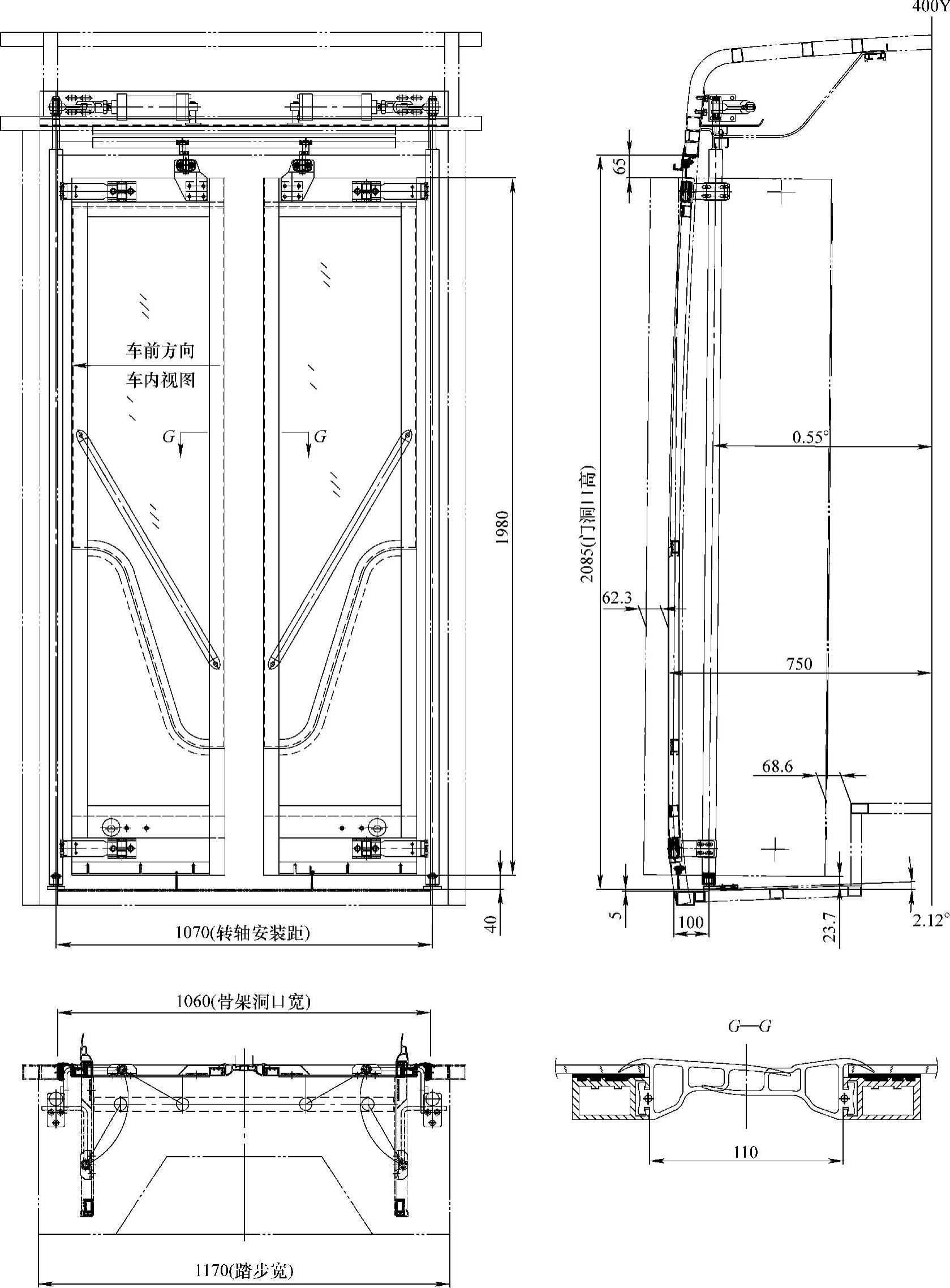
图5-59 外弯臂型双内摆乘客门

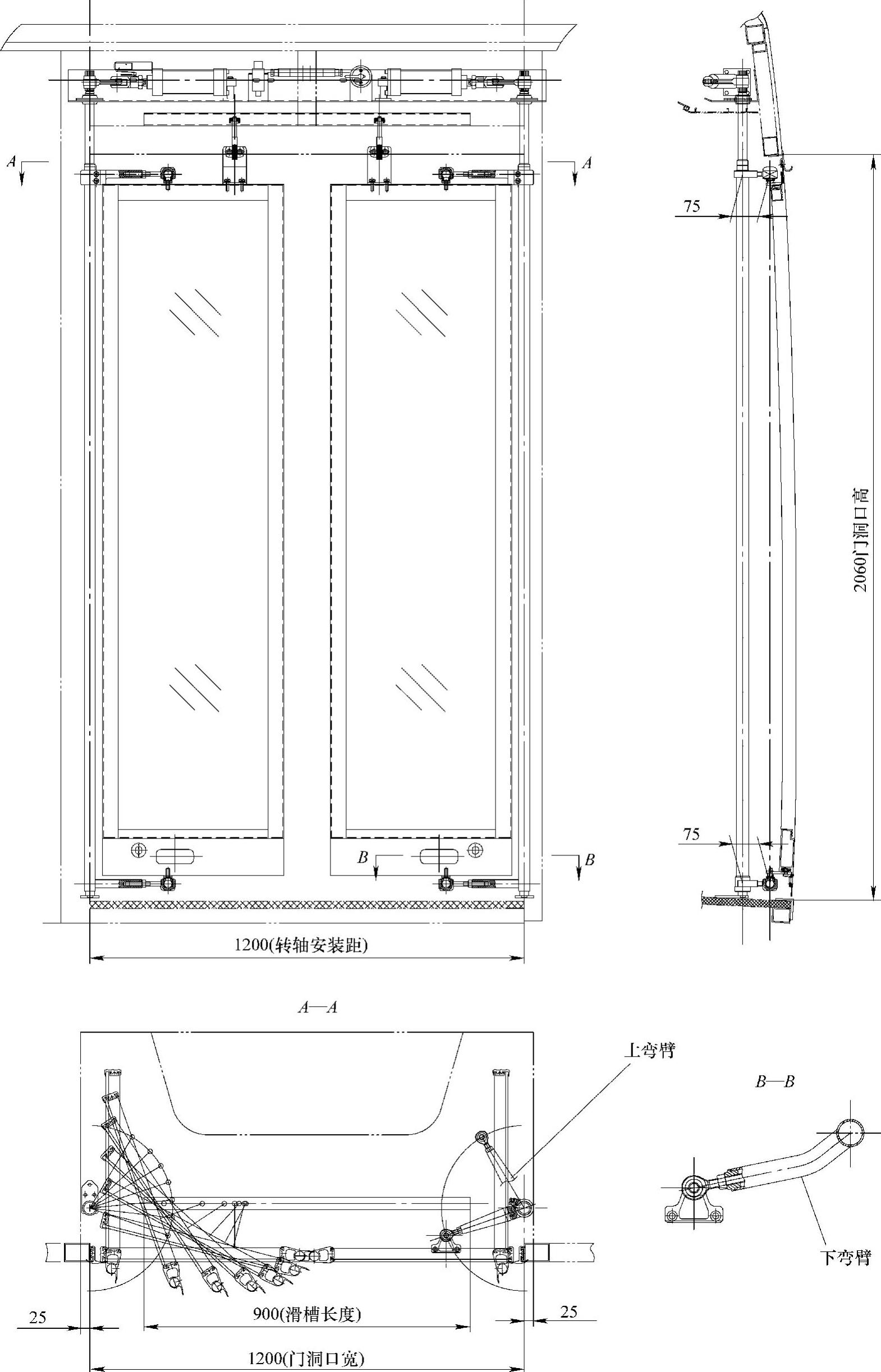
图5-60 内弯臂型双内摆乘客门