7.2.2.1 波浪模型试验
1)试验目的及内容
通过波浪断面物理模型试验[34],在各种工况条件下研究结构各部分最大波压强分布,计算出波浪总力,为结构形式的选择和尺寸优化提供参考依据。
2)模型设计
上筒顶高程为+7.0m,以上设胸墙。胸墙形式分为弧形,其结构图如图7-5所示。模型比例尺仍取1∶20,桶体模型用钢板制作。
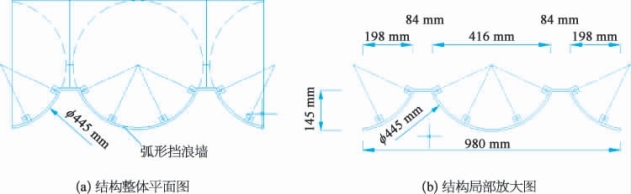
图7-5 弧形胸墙结构示意图
3)试验组次
测量波压力的试验组次见表7-4。
表7-4 试验组次

注:堤前泥面高程为-5m,堤前水深从泥面高程起算。
4)波浪力试验结果
表7-5给出了规则波作用下胸墙在各种水位时最大波压力的试验结果。
表7-5 波压力试验结果

7.2.2.2 桶式基础结构数值分析
为进一步深入研究桶式基础结构的整体稳定性,本次设计以ABAQUS有限元软件为平台,建立结构的三维弹塑性有限元数值模型和非线性弹塑性的三维桶式基础结构与土共同作用的计算模型,考虑各种工况组合下波浪动载对结构与土的动力响应。
1)模型简介
极端高水位(6.56m)条件下,1%波高(6.72m)对应的波浪力作用在上部结构时,进行桶式基础的稳定性分析。图7-6为桶式基础结构的平面布置图,由于桶式基础结构布置的对称性,选取图中阴影部分区域为计算区域。该区域宽10.5m,长度方向取3倍桶式基础结构长边的长度为90m。模型分析关注的是桶式基础结构在淤泥土地基上的稳定情况,为减少计算量,取地基土计算厚度为25m(标高为-5~-30m),其中上部淤泥层厚度为8.5m(标高为-5~-13.5m),下部16.5m厚土层(标高为-13.5~30m)按粉质黏土考虑。桶式基础结构上筒高15.1m、下桶高9.0m。
桶式基础结构面与地基土之间设置接触面,指定结构上的接触面为主接触面、土体接触面为从接触面。接触面间采用库伦摩擦模型,结构面与淤泥间的摩擦系数为0.04,结构面与粉质黏土间的摩擦系数为0.2。接触面法向采用硬接触方式。
桶式基础结构采用弹性模型,重度γ取25kN/m3,水面以下浮容度γ′取15kN/m3,弹性模量为3×104 MPa,泊松比ν取0.167。
地基土的本构模型分别采用摩尔-库伦模型(M-C模型)和扩展的Drucker-Prager模型(D-P模型)进行模拟,分析过程采用总应力法,土体参数指标取快剪指标。
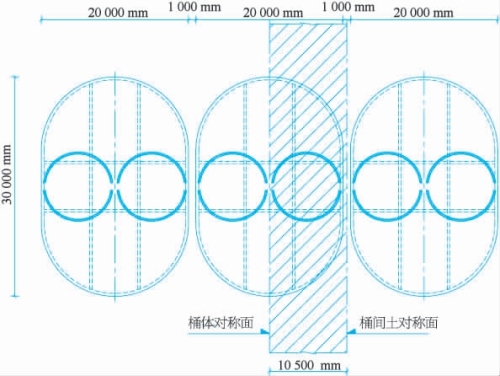
图7-6 桶式基础结构平面图
2)稳定性分析步骤
采用有限元方法进行波浪力等荷载作用下圆结构稳定性分析的步骤如下:(1)建立有限元分析模型。
(2)根据波浪力等荷载的分布,在结构上逐级加波浪荷载,采用有限元分析模型计算不同加载荷载时对应的土与结构体系的位移和应力,加载至有限元计算不收敛。
(3)绘制荷载-结构位移关系曲线。
(4)依据荷载-结构位移关系曲线确定判别结构失稳的准则。(https://www.xing528.com)
(5)根据失稳判别准则,确定结构稳定性破坏对应的荷载,该荷载定义为结构的极限承载力。
(6)将结构极限承载力与设计荷载的比值定义为稳定性安全系数。
3)加载系数
为清楚表达计算时施加荷载与设计荷载的关系,定义一个表征加载程度的加载系数α,对荷载加载值进行无量纲化处理:
![]()
式中 P——计算时施加的荷载;
PD——设计荷载(计算的波浪作用力)。
当P加载到结构极限承载力Pu时,若加载系数α<1,表明结构极限承载力小于设计荷载,结构是不安全的;若加载系数α=1,表明结构极限承载力等于设计荷载,结构处于极限状态;若加载系数α>1,则表明结构极限承载力大于设计荷载,结构是安全的。故当P加载到结构极限承载力Pu时,加载系数α可定义为结构稳定性安全系数K。
4)失稳判别准则
可参照以下两个准则来判别桶式基础的稳定状态:
(1)标准Ⅰ:极限承载力作为判别标准。以P-S曲线斜率接近于零时对应的波浪力作为极限承载力。若土体本构关系为理想弹塑性模型,根据理想塑性流动概念,此时即使波浪力增加很小,结构也将产生非常大的位移值,说明结构此时已发生破坏。
(2)标准Ⅱ:基于P-S曲线出现较明显拐点作为稳定性判别标准。在波浪力值不是很大的情况下,大部分土体处于弹性状态,P-S曲线大体为线性。当作用的波浪力值继续增大,进入屈服的土体单元增多,土体的塑性区逐渐扩展。当塑性区扩展到一定程度时,结构位移增加幅度变快,P-S曲线出现较明显拐点,结构稳定性受到威胁。
5)结构转角θ的定义
对于结构转角θ的推导如下:由于结构整体刚度远大于软土地基,可以将其看成刚体,则结构转角θ可由结构在竖直方向上两任意点(图7-7中的A点与B点)的水平位移和两点之间的距离L推导得出,即
![]()
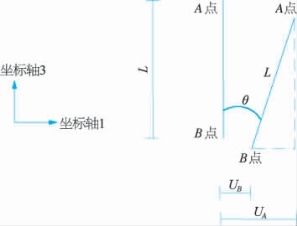
图7-7 结构转角θ公式推导示意图
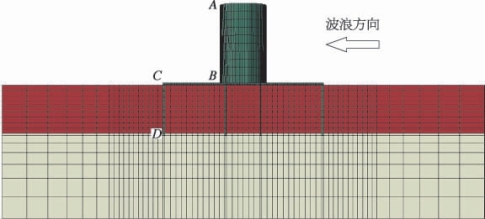
图7-8 模型关键点分布示意图
图7-8中A、B、C、D四点为本次分析过程中选择的桶式基础结构关键点。后续分析过程中将给出这些关键点在波浪力作用下的位移变化情况,根据上述各点位移来计算不同波浪荷载下的结构转角。由于桶式基础结构刚度远大于土体刚度,在波浪力作用下,结构体变形较小,因此根据A、B点计算出的转角应与C、D点计算结果一致。

图7-9 关键点A~D的Y方向位移曲线
6)计算结果
首先对位移量U1~U3的方向做如下说明:U1方向与桶式基础结构短轴方向一致(X方向)、U2方向与桶式基础结构长轴方向一致(Y方向)、U3为竖直方向(Z方向),位移单位均为m。绘制位移与加载曲线,如图7-9~图7-11所示。
综上所述,根据各曲线得到的安全系数:U2方向为1.78,U3方向为1.88,结构转角θ为1.68。
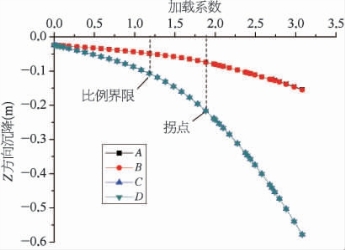
图7-10 关键点A~D的Z方向位移图
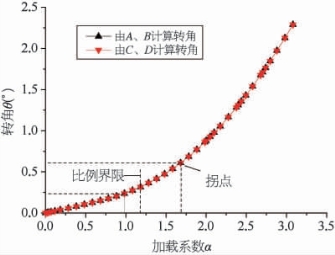
图7-11 桶体转角随加载变化曲线图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




