3.3.1.1 计算前提假设条件
桶式基础结构稳定性计算分析是基于新创建的条件极限平衡计算方法。该方法的基本思路是:假设结构与其所约束的桶内土体产生刚体小转动,合力中心位置不因转动而发生改变,桶内土体参与抗倾计算的重量根据真空度和桶壁摩擦力确定;结构的竖向和水平向极限平衡互不影响;极限弯矩平衡是根据地基承载力的极限分布形式计算,计算方法如图3-1所示。其计算步骤为:
(1)转动趋势判断。对结构取隔离体,把结构和结构内土体看成刚体放在刚性地面上,刚性面以上的外荷载平移到结构底面中心上,计算合力矩,确定结构偏转方向。
(2)计算水平和竖向的合力,计算地基反力。
(3)根据极限承载力和地基反力,计算极限弯矩平衡下地基反力分布形式。
(4)计算地基反力的合力,并计算与竖向合力形成的极限力矩。
(5)计算绕底面转动点O(或底面中心)的极限抗倾力矩与绕底面转动点O(或底面中心)的倾覆弯矩比值(抗倾安全系数),判定结构是否安全。
3.3.1.2 转动中心计算
转动中心位置可以根据数值分析或试验结果确定,规则结构也可以通过简化计算方法确定,计算示意如图3-2所示。当桶式基础平面为矩形时,转动中心设置在桶底面,转动中心距倾覆侧桶壁的距离可按式(3-4)计算。(https://www.xing528.com)
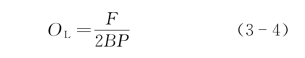
式中 OL——转动中心距倾覆侧桶壁的距离(m);
F——计算地基面上的竖向荷载(kN),包括结构自重、桶式基础内土体自重、外荷载等;
B——桶式基础转动轴方向水平截面宽度(m);
P——地基极限承载力竖向应力平均值(kPa),按现行行业标准《水运工程地基设计规范》(JTS147—2017)的有关规定执行。
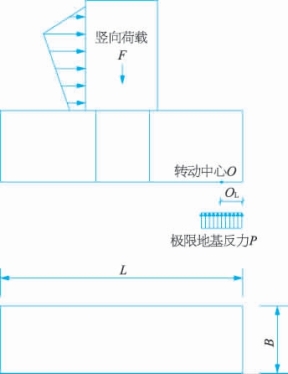
图3-2 矩形截面转动中心计算示意图
L—桶式基础有效计算长度(m);O—转动中心点
当桶式基础平面为非矩形时,可按转动轴方向的结构宽度等面积折算为矩形进行转动中心位置计算。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




