水运工程桶式基础结构技术：钢桶屈曲分析

2.3.2.1　基本荷载作用下钢桶屈曲特性

在实际施工过程中，桶体的基本荷载包括轴压、围压、自重、顶力、摩擦力等。根据实际施工情况，提取了两种基本荷载，即轴压和围压，这是施工过程中最主要的受力。采用数值分析时，做以下设定：

（1）数值分析中建立的桶体模型，不考虑土层的影响和桶、土相互作用。

（2）采用Q235钢的参数作为计算的基本参数，不考虑桶体本身的自重。

（3）桶体稳定性分析的基本模型尺寸为：桶径d＝3m，壁厚t＝14mm，长L＝17m。

1）轴向压缩荷载作用

在轴向压缩条件下，采用钢桶一端固结、一端直接施加轴向压力的边界条件，分析钢桶受力结果见表2-8。由表可见，有限元计算结果与理论值符合得较好。

表2-8　理论值与有限元计算值对比

（续表）

在上述弹性计算的基础上，将相应的模态作为几何缺陷加入弹塑性屈曲计算。将轴压一阶模态作为钢桶几何缺陷，取0.01倍桶径作为几何缺陷的变形量，引入缺陷后计算结果为极限承载力，见表2-9。表中极限承载力折减后的值是极限承载力和有限元计算值之比，钢桶屈服理论值为Py＝σyA（A为桶口截面面积）。

表2-9　轴压作用下计算结果

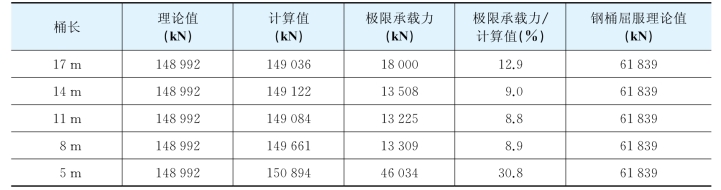
由表2-9可知，当引入几何缺陷后，极限承载力降低很多，甚至会显著低于钢桶的屈服理论值，在钢桶未发生屈服时，便已经有屈曲失稳的可能，此时若仍然使用屈服荷载进行设计便可能发生危险。因此，对桶体进行加筋以提高其极限承载力是很有必要的。

2）围压荷载作用

围压工况对钢桶施加两端简支的边界条件，对桶体施加围向压力，结果整理见表2-10。由表中数据可知，有限元计算值与短管理论值接近，长管理论值较小。

表2-10　围压作用计算结果

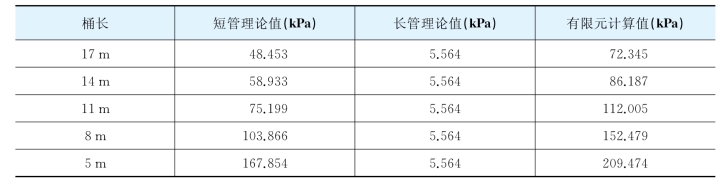
在上述弹性计算的基础上，将相应的模态作为几何缺陷加入弹塑性屈曲计算。以0.01倍桶体壁厚为几何缺陷的比例因子，引入缺陷，计算得到的荷载比例因子与弧长关系如图2-25所示。由图可知，引入几何缺陷后的桶体，其极限承载力会折合为临界荷载的50%左右。

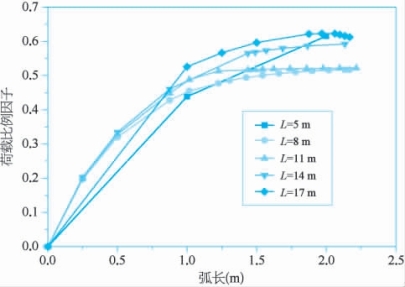
图2-25　荷载比例因子与弧长的关系

3）轴压和围压联合作用

为了研究径向荷载对轴压的影响，对17m钢桶进行弹塑性分析，分别研究钢桶在无围向压力和围压作用下钢桶的荷载位移关系，围压大小设置为1000MPa，计算得荷载位移关系如图2-26所示。

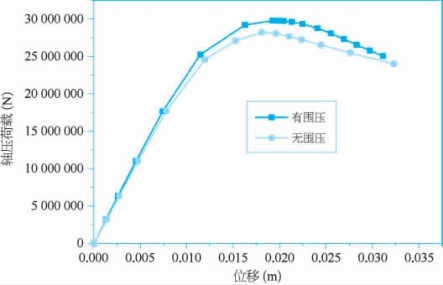
图2-26　荷载位移曲线图形分析

由图2-26可知，起初位移较小时，荷载位移近似为线性关系；当荷载达到一个峰值以后，钢桶承载力明显下降。这是符合客观事实的，同时可以看出，轴压和围压的共同作用可以提高桶体的极限承载力。(www.xing528.com)

2.3.2.2　加筋桶数值模拟

钢质桶体的加筋有不同的布置形式，为提高轴向承载力可以布置纵向加筋，为提高径向承载力可布置环向加筋，用于提高屈曲承载力。采用桶长17m的桶体进行加筋研究，探究加筋数量对钢桶屈曲承载力的影响。

1）载荷和边界条件

根据工程中该类结构的实际受载情况，确定数值模拟时的边界条件为：上端面约束除轴向位移外的所有自由度，下端面固支约束。同时通过定义带参考点的控制来施加轴压，试件上端面与钢板之间定义接触约束来传递轴向载荷。

2）静力分析

对长度为17m的加筋钢桶进行弹塑性分析，观察加筋形式对桶体承载力的影响。实际工程中桶体的加筋情况：钢桶下部3m采用20cm高的T型钢进行竖向加强，共45处，加强间距为0.42m；其余部分采用20cm高的L型钢进行环向加强，加强间距为2.0m，荷载为2260.8kN。

从桶盖应力计算结果分析，对于桶体来说，整体受力较小，并未发生屈服，中间部分内力较大，应力值达到了1.48MPa，远远小于屈服应力。对于桶体整体受力也较小，未发生屈服，上部内力较大，应力值达到了10.54MPa，远远小于屈服应力。从轴向和径向的内力分析，轴向内力和径向内力值都很小，变形最大的地方也只发生了0.803mm的变形，钢桶结构非常安全。

3）后屈曲分析

上述静力分析弹性承载力钢桶的实际承载力，因为其未考虑材料非线性及几何非线性，真正计算钢桶承载力需要将几何缺陷加入钢桶模型，并考虑材料的塑性。下面对比桶高17m时，光桶和加筋桶的临界荷载、加入几何缺陷和非线性后的极限荷载。

实际工程中桶体的加筋情况：钢桶下部3m采用20cm高的T型钢进行竖向加强，共45处，加强间距为0.42m；其余部分采用20cm高的L型钢进行环向加强，加强间距为2.0m。

将一阶模态的临界荷载分别加到光桶和加筋桶上，进行有限元计算。根据有限元计算结果，将光桶引入几何缺陷后，利用弧长算法计算出弧长和荷载比例因子的关系，绘制成图2-27。根据绘制的弧长-荷载比例因子的图像可以看出，在引入初始几何缺陷后，荷载折减为临界荷载的11%，初始几何缺陷大大降低了光桶的承载力。

根据有限元计算结果，将加筋钢桶引入几何缺陷后，利用弧长算法计算出弧长和荷载比例因子的关系绘制成图2-28，荷载折减为临界荷载的18.4%，相对下降幅度增大。

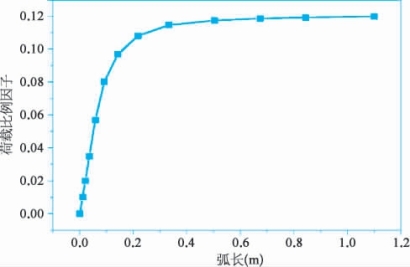
图2-27　光桶引入几何缺陷后弧长与荷载比例因子的关系

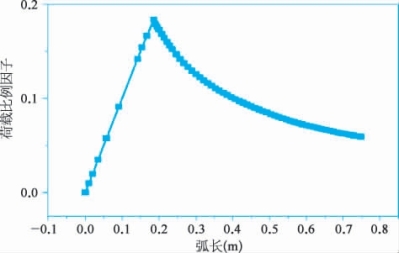
图2-28　加筋桶引入几何缺陷后弧长与荷载比例因子的关系

4）纵向加筋数量的影响

计算采用的模型由蒙皮和筋条组成，筋条采用纵向均布，蒙皮厚度t＝14mm，壳半径R＝3m，长度L＝17m，弹性模量E＝2×105 MPa，泊松比ν＝0.3。薄壁加筋壳结构进行有限元分析时，蒙皮和筋条采用绑定接触处理；桶体底边进行固支约束，两侧进行对称约束，顶端施加均布载荷，建立结构的计算模型。

分别对加筋条数n＝0、5、15、25、35、45的桶体进行计算，得出各自的临界荷载并绘制曲线，如图2-29所示。

由图2-29可知，加筋条数为n＝0、5、15、25时，加筋桶的临界荷载明显变大，而加筋条数n为25、35、45时，临界荷载几乎没有增大。因此，加筋条数并不是越多越好。

5）环向加筋数量的影响

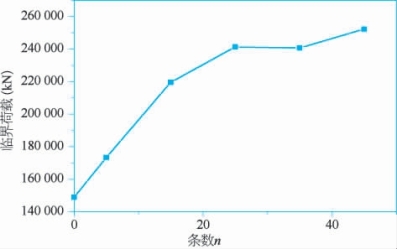
图2-29　临界荷载随加筋数量的变化

计算采用的模型由蒙皮和筋条组成，筋条采用环向均布，蒙皮厚度t＝14mm，壳半径R＝3m，长度L＝17m。薄壁加筋壳结构进行有限元分析时，蒙皮和筋条采用绑定接触处理；桶体底边进行固支约束，两侧进行对称约束，环向施加均布载荷，建立结构的计算模型。分别对加筋间距为1m、1.5m、2m、2.5m、3m、3.5m的桶体进行计算，得出各自的临界荷载并绘制曲线，如图2-30所示。

图2-30　临界荷载随加筋间距的变化

由图2-30可知，环向筋间距为2.0～3.5m时，加筋桶的临界荷载明显变大；环向筋间距为1.5～2.0m时，临界荷载几乎没有增大；环向筋间距为1.0～1.5m时，临界荷载又明显增大。因此，本工程的钢桶环向筋间距为2.0m就可以满足要求。