2.5.1 船舶阻力
集装箱船KCS和6 000 TEU在不同工况下航行的阻力计算值如表3-3所示。可以看出:在船体与浮泥接触之前,随着龙骨下富裕水深的减小,船舶阻力略有增加;当船底与浮泥刚有接触,此时富裕水深为零,与之前正值的富裕水深相比,船舶阻力呈现跳跃式地增加;当富裕水深变为负值后,随着浮泥厚度进一步增加,船舶阻力平稳地增加。当船舶吃泥深度为0.2倍船舶吃水时,与没有浮泥情况相比,船舶阻力增大了约5倍,但该值与船舶在深水中以服务航速航行时的阻力值相比,只有后者的一半。因此,船舶阻力随着浮泥厚度(即吃泥厚度)增加而增加。
油轮KVLCC2在不同浮泥厚度下航行的阻力值如图3-13所示。可知,在船舶富裕水深为-0.1,即船舶吃泥深度达到0.1倍吃水之前,阻力的变化与泥厚的变化几乎为线性关系;在船舶吃泥深度超过0.1倍吃水之后,随着吃泥厚度进一步增大,阻力变化幅度迅速增大,变化趋势呈现出非线性。当浮泥厚度为0.2倍吃水时,即船底面跟浮泥刚有接触,此时船舶阻力为31.27 N;当浮泥厚度为0.3倍吃水时,即船舶吃泥深度为0.1倍吃水,此时船舶阻力为42.56 N;当浮泥厚度为0.4倍吃水时,即船舶吃泥深度为0.2倍吃水,此时船舶阻力为70.87 N。以上分析表明,这种船型的船舶阻力同样随着浮泥厚度,即吃泥厚度的增加而增加。
表3-3 KCS和6 000 TEU船阻力计算结果
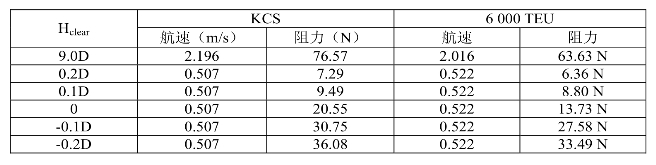
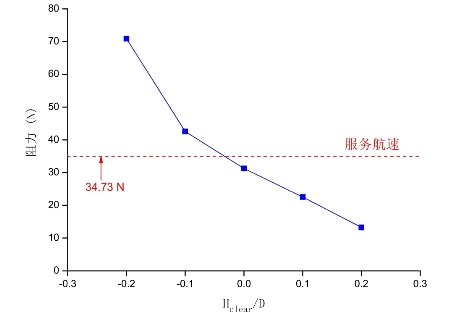
图3-13 KVLCC2船型在不同富裕水深下阻力(其中,服务航速为1.177m/s)
2.5.2 交界面波动
通过数学模型模拟上述三艘船型在不同浮泥厚度下航行时引起的水-浮泥交界面波动情况,其中KCS船型如图3-14至图3-17所示。可以看出,交界面波动幅度随船舶吃泥深度变化而变化。对于吃泥深度为0.2倍吃水的情况,交界面最大波谷出现在船首,波动向船尾方向逐渐减少。KCS和6 000 TEU集装箱船波面下降约为船长的2‰,交界面最大波峰出现在距离船首1/3到1/2位置处,波面升高约为船长的5‰。KVLCC2油轮波面下降约为船长的1.2%,交界面最大波峰出现在离船首1/4倍的船长处,波面升高约为船长的1%。对于其他吃泥深度的情况,除了交界面波动幅度减少外,交界面波形变化与吃泥深度为0.2倍吃水的情况类似。(https://www.xing528.com)
以上计算结果表明,船舶在浮泥水域中航行会引起水-浮泥交界面波动,并且交界面波动随船舶吃泥深度增大而增大。另一方面,由于水-浮泥交界面波动幅度很小,对船舶阻力增加的贡献有限,说明船舶在浮泥中航行阻力变化主要还是由于流体黏度发生变化引起的。在浮泥与船底接触前,存在于航道底部的浮泥黏度大于上层的清水黏度,造成航道底部流体的流动性比上层流体的流动性要差,相当于航道的堵塞效应增大,从而使得船舶阻力增加;在浮泥与船体接触后,由于流体的黏性增加,直接造成船舶的摩擦阻力增大,再加上堵塞效应的影响,造成船舶阻力迅速增加。
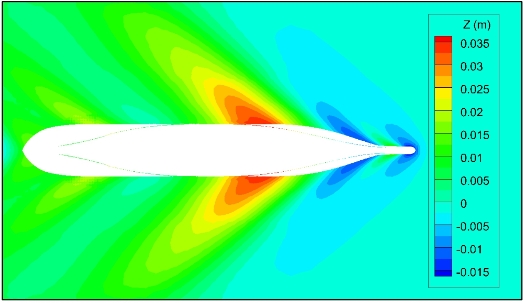
图3-14 KCS船型水-浮泥交界面波动(Hclear=-0.2 D)

图3-15 KCS船型水-浮泥交界面波动(H Hclear=-0.1 D)

图3-16 KCS船型水-浮泥交界面波动(Hclear=0)

图3-17 KCS船型水-浮泥交界面波动(Hclear=0.1 D)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




