钢板砖砌组合加固改造试验与应用成果

前面已经介绍了钢板－砖砌体组合梁可能发生的两种破坏模式，即弯型破坏和扭型破坏。本小节主要针对组合梁发生扭型破坏时，利用钢板小挠度弯曲理论分析其破坏过程，并给出相应的计算公式。

1）钢板的小挠度弯曲问题

（1）相关概念和求解方法探讨

当板的厚度t远小于另外两个边的最小尺寸b（小于b/8至b/5）时，则称该板为薄板［7］。薄板的小挠度弯曲理论指出，薄板虽然很薄，但仍然具有相当的弯曲刚度，因而它的挠度远小于它的厚度（小于板厚的1/5）。钢板－砖砌体组合梁在受力过程中，侧板受到平面外拉力与内部核心砖砌体的支承作用，使得钢板发生平面外的挠度，该挠度值在对拉螺栓达到屈服时远小于侧板厚度，因此其可用薄板的小挠度弯曲理论进行分析。薄板的小挠度弯曲理论是以三个计算假定为基础的。取薄板的中面为xy面，这些假定如下：

①垂直于中面方向的正应变可以不计，即εz＝0；

②应力分量τzx、τzy和σz远小于其余三个应力分量，其引起的形变εz、γzx、γyz可以不计；

③薄板中面内的各点都没有平行于中面的位移，即uz＝0＝0，vz＝0＝0。

由上述三个假定并结合几何方程、物理方程有：

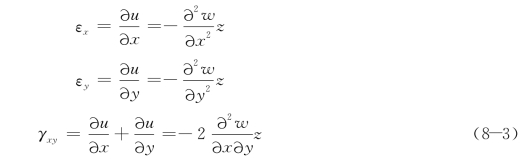
及

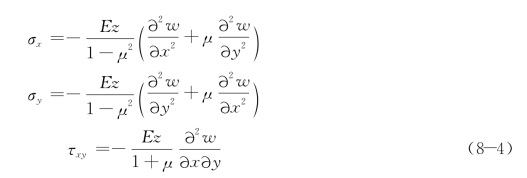
结合薄板的上表面的边界条件，则有：

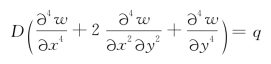
简写为

其中：w为薄板的挠度；μ为泊松比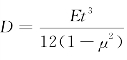；为钢板的弯曲刚度；E为钢板的弹性模量；t为钢板的厚度。

对于薄板的小挠度理论的求解方法有很多种［63］：精确求解的纳维解法、莱维解法、差分法以及变分法的里茨法、伽辽金法等。其中变分法是解决实际问题很有效的方法，这里将主要介绍变分法的里茨法和伽辽金法，并比较其优缺点。

在薄板的小挠度弯曲问题中，由于不计形变分量εz，γzx，γyz，因此形变势能的表达式简化为：

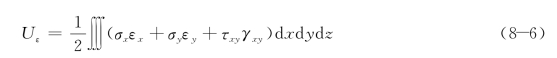
将公式（8－3）的形变分量和公式（8－4）的应力分量代入上式，并注意到w是（x，y）的函数，对z进行积分，从－t/2到t/2，得出薄板的形变势能为：

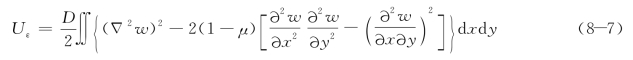
薄板在横向荷载作用下的外力功和外力势能为：

因此，薄板弯曲问题的总势能极值条件是：

求解薄板弯曲问题的里茨法是首先设定挠度函数w的试函数：

其中Cm为互不依赖的m个待定系数；wm为满足薄板位移边界条件（关于挠度及转角的条件）的设定函数。这样，不论Cm如何取值，上式所示的挠度w总能满足位移边界条件。然后再满足里茨变分方程

由此可以得出Cm的m个线性方程，从而可解出系数Cm。

求解薄板弯曲问题的伽辽金法：令设定的挠度函数必须同时满足位移边界条件和内力边界条件（关于弯矩和总剪力的条件），也就是必须同时满足薄板的全部边界条件，同时还应当注意，设定的挠度函数尽可能不要使其在任何边界上满足实际上不存在的位移边界条件或内力边界条件，以免得出不精确甚至不合理的结果。然后再满足伽辽金变分方程：

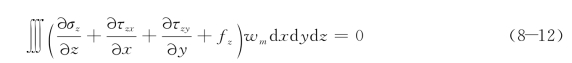
其中，在薄板的弯曲问题中，体力fz是归入为横向荷载q的，因此公式（8－12）中应当取fz＝0。此外注意到wm只是x和y的函数，不随z而变，则公式（8－12）可以写成：

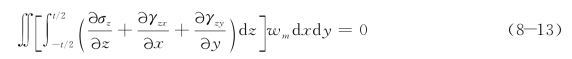
分别对z进行积分，得出薄板的伽辽金变分方程为：

由此可得m个方程，用来求解系数Cm。

与里茨法相比，伽辽金法中假定的挠度函数w不但需要满足位移边界条件，而且要满足内力边界条件，这增加了挠度函数构造的难度，尤其是在边界条件比较复杂时。因此，这里采用里茨法来求解薄板的小挠度弯曲问题。

（2）数学模型建立

根据前面的试验和文献［64］的有限元分析结果，得知组合梁在受力过程中，钢板发生平面外受拉的主要区域如图8－19中实线所示。为便于分析，将钢板受力区域作一些简化，取1#螺栓之间、高度为a的钢板作为计算单元。螺栓的布置对钢板的变形有一定的抑制作用，但是作为计算单元的钢板竖向只有两排螺栓，对钢板的变形限制有限，螺栓之外的钢板也是可以发生平面外挠度，这与试验现象及有限元分析是相吻合的［64］。因此，若将左右边界简化为固结约束是偏于不安全的，此处偏于安全考虑将其视为简支约束。计算单元的上边的边界条件是自由边，而钢板平面外挠度并未发展到组合梁底部，因此可以将底边的边界条件视为固结约束。此外，计算单元受到的平面外力是呈梯形分布的不均匀面荷载，但是出于简化计算，将荷载视为大小相同的均布面荷载，具体如图8－20所示。

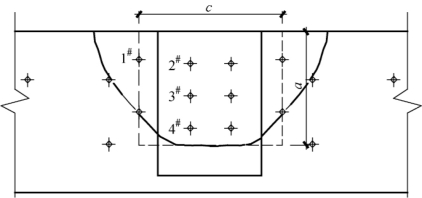
图8－19　钢板受力区域及简化图

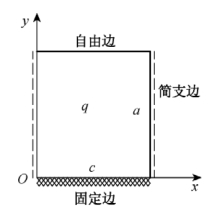
图8－20　钢板受力边界示意图

基于上述分析，对于两边简支、一端固结和一边自由的矩形钢板，其位移边界条件为：

当x＝0或c时，w＝0；

当y＝0时，w＝0且；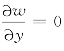

当y＝a时，w≠0。

采用里茨法时，挠度函数只需要满足位移边界条件，因此可以设挠度函数表达式为：(www.xing528.com)

公式（8－15）完全能够满足上述的位移边界条件。

（3）钢板的形变势能

按照公式（8－15）求出钢板挠度w对于坐标的二阶导数，得到：

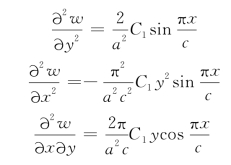
将上述挠度函数的微分式代入公式（8－7），对x，y进行积分并化简，可求得：

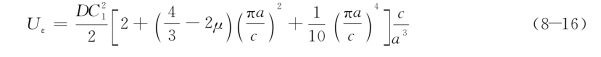
从而得到：

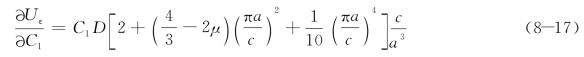
另一方面，由公式（8－15）得到：

将公式（8－17）、公式（8－18）代入公式（8－11），可求得C1，再代入公式（8－15）和公式（8－16），可以得到：

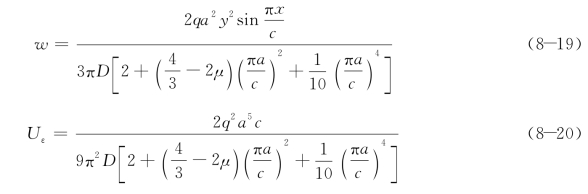
对于计算单元上与2#螺栓同一高度、加载端与侧板连接点坐标为（c－50，a－80），将其代入公式（8－19），考虑到2#螺栓的伸长值Δ2，可以求得均布面荷载q的表达式，再代入公式（8－20），从而得到计算单元的形变势能：

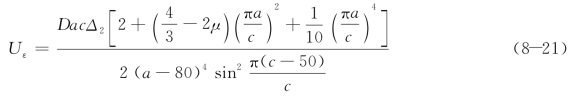
其中，a＝k1h；h为组合梁的高，由有限元分析结果可取k1＝0.7；c＝k2b，b为组合梁的宽，k2＝1.458；μ为泊松比，对于钢板取值0.3，代入公式（8－21）则有：

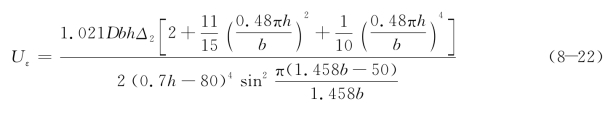
式中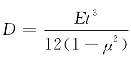，为钢板弯曲刚度；E为钢板的弹性模量；t为钢板的厚度；Δ2为2#螺栓的伸长值。

2）螺栓拉伸的应变能及外力势能

根据试验和有限元模拟分析结果［64］，组合梁在受力过程中，受力螺栓主要分布在加载端的范围内，即其余螺栓受到的力很小，可以忽略不计。受力螺栓的分布见图8－19中实线部分；且对拉螺栓以受轴力为主，弯矩和剪力的作用影响也很小。依据前面的假定，可认为竖向螺栓之间的伸长值是线性关系，具体见图8－21所示。

由于加载外伸梁内填充物为混凝土，导致其刚度很大，因而组合梁在加载端底部位置的砖砌体受到压力作用而压溃，导致加载端的底部凹陷到组合梁上，这与有限元分析的结果是一致的（图8－22）。图8－21中a的取值与前述小节中相同，即a＝0.7h，加载端的螺栓布置是已知的，由几何关系可知图8－21中螺栓的伸长量以及外荷载作用点的竖向位移：

图8－21　加载端位移关系示意图

图8－22　有限元模型加载端位移示意图

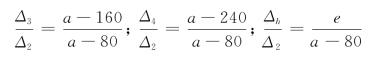
于是可得：

对于同一高度范围内对拉螺栓之间的伸长量，可以简化为如下的薄壁梁：该薄壁梁高为钢板厚度t，以加载端两侧对拉螺栓A、A′作为固定边，之间的螺栓简化为弹簧支座，而与加载端同宽的该部分钢板视为弯曲刚度无限大。该简化梁示意图及荷载作用下变形曲线见图8－23所示。其中，l1、l2是加载端处对拉螺栓的间距，分别为l1＝75mm，l2＝50mm。

对于薄壁梁的变形曲线，知道其AB段位移函数需满足边界条件f（0）＝0、f′（0）＝0、f′（l1＋l2）＝0、f（l1＋l2）＝Δ2，因此假设变形曲线的位移函数：

f（x）＝a1x3＋a2x2＋a3x＋a4

将上述边界条件代入上式，考虑到加载端的螺栓布置不在此研究内容中，因此将l1、l2用数值代入计算，经计算并简化后得AB段位移函数为：

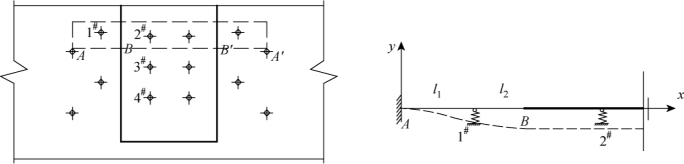
图8－23　薄壁梁及变形曲线示意图

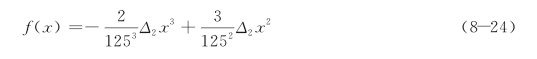
于是可以得到1#螺栓的伸长值：

对于长度为l的单向拉压杆件，杆件的拉伸应变能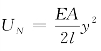；则加载端范围内螺栓的拉伸应变能为：

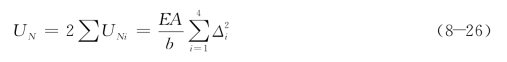
图8－21所示的外荷载势能为：

3）组合梁的屈服承载力

根据能量原理U＋V＝0，将公式（8－22）、（8－23）、（8－26）、（8－27）联立求解，并注意到组合梁的扭矩，则2#对拉螺栓达到屈服应变时，即Δ2＝εyb时组合梁的屈服承载力为：

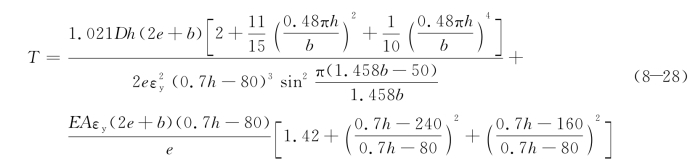
式中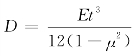：为钢板弯曲刚度，E为钢板的弹性模量（mm4）；t为钢板的厚度（mm）；e为外荷载加载点至组合梁侧边的距离（mm）；h为组合梁的高度（mm）；b为组合梁的宽度（mm）；A为对拉螺栓的截面面积（mm2）；εy为对拉螺栓的屈服应变。

由于在本次试验中没有测得对拉螺栓何时屈服，因此理论计算值无法直接与试验值进行对比。因此，这里选择理论计算值与有限元模型中的值进行对比［64］，具体见表8－6所示，表中未列出的其余参数相同，均为b＝240mm，h＝400mm，e＝340mm，εy＝0.003 16。

表8－6　理论计算值与有限元分析值比较结果

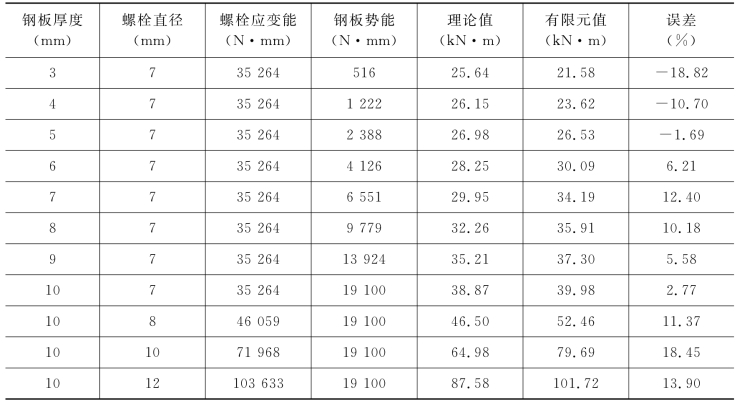
从表8－6中可以看出，理论计算得到的屈服承载力与有限元分析值较接近。除了钢板厚度较小的组合梁，其余的屈服承载力的理论计算值均小于有限元分析值，说明公式（8－28）能够偏安全地预测组合梁的承载力。此外，从该表中还可以看出对拉螺栓的直径变化对于承载力的影响较大。