规则波中船舶的平均波浪增阻是纵向二阶力的定常部分，而忽略了二阶速度势的影响后，主要是一阶势对二阶力的贡献。通过船舶在波浪中航行时的流场特性以及速度势的线性分解，为方便计算和分析，通常认为波浪增阻主要可以被分为辐射波引起的波浪增阻和绕射波引起的波浪增阻。从能量的角度来看，波浪增阻可以理解为船舶在波浪激励下运动而产生的波所带走的能量。而且由于船体的存在，能量是通过辐射波和绕射波的形式带走的。
文献［64］认为总的波浪增阻可以表达为
式中，R aw_R为辐射波浪增阻；R aw_D为绕射波浪增阻。这两部分将采用不同的方法分别计算。
1）运动辐射增阻
在12.6.1节所述的几种方法中，经过大量的数值验证可知，辐射能量法无论是在适用性还是准确性上都较为令人满意，所以辐射能量法在工程中有着广泛的应用。故可以预计在三维面元法的框架下采用辐射能量的思想计算波浪增阻也会有着不错的效果。
假定在规则波中航行的船舶在六个自由度的运动有如下的形式：
式中，x k、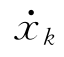
和
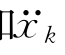分别为船舶在第k个自由度上的运动位置、速度和加速度，X kR和X kI分别为第k个自由度上运动幅值的实部和虚部。那么在一个遭遇周期内船体辐射出去的能量应该与辐射力所做的功相等，则辐射能量E有如下表达：
式中，F j为第j个自由度上的广义辐射力，通过之前的推导可知，辐射力与船舶水动力系数附加质量μjk和阻尼系数λjk有如下关系：
将式（12.91）和式（12.93）代入式（12.92），则
考虑到下列关系的存在：
则辐射能量E有如下的最终表达：
根据式（12.84）所示的辐射能量和波浪增阻的关系，可得到波浪增阻的表达如下：(www.xing528.com)
需要说明的是由于辐射能量的成分中仅包含了辐射波所传递的能量，所以式（12.97）的计算结果是辐射增阻，除了短波工况，其在总增阻中均为主要部分。相较于G＆B的二维辐射能量法的表达，可以看到式（12.97）可以将六个自由度对波浪增阻的影响都考虑进去，这便于计算非迎浪情况下不同运动模态对波浪增阻的影响，同时附加质量对波浪增阻值的影响也被计算在内。可以认为本三维辐射能量的表达比G＆B的更为完善。
关于零航速的情况，由于存在关系A jk=A kj，所以式（12.97）中方括号中的第一项，即与附加质量相关的这一项经过求和后可以证明其值为0，同时波浪频率与遭遇频率相同，那么式（12.97）在零航速时的表达式为
若仅仅考虑垂荡和纵摇模态的影响，式（12.87）与Joosen法的表达是完全一致的，而在考虑航速影响时，Joosen法仅仅是用遭遇频率代替波浪频率进行计算，这与式（12.97）所示的有航速时的表达并不一致，这可能是Joosen法在计算有航速问题时的误差来源之一。
需要注意的是，如式（12.96）所示，辐射能量E是通过船舶在波浪中运动时船体与波浪间的相互作用产生的。采用三维面元并求解船舶运动方程，可以获得船舶在波浪中摇荡运动的幅值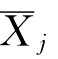
，但是这个运动幅值
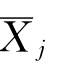是相对于静水中船舶的平衡位置而言的。在实际运动中，由于船体周围自由波面的变化使得船舶在波浪中运动时船体与波浪之间的相互作用比静水中强迫振荡时更多。故计算辐射能量时，在考虑船体周围波面变化的影响后需要对船舶运动结果加以修正。这同时也是对FroudeKrylov假定的一种修正。在G＆B的辐射能量法中，对于每一个切片处船舶二维剖面的垂荡运动都进行了修正。那么仿照G＆B的做法，在三维计算中，可采用对船舶重心处垂荡运动的修正来表征整船相对于波浪的运动，其表达式如下：
式中，T*为船舶平均吃水，可用近似计算为：
，Δ为船舶排水体积，A W为水线面面积。这样，修正后的船舶垂荡运动幅值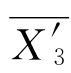
则可以表达为
2）绕射增阻
绕射波对阻力增加的贡献更多地体现在波长较短的入射波作用下，而在上节所述的常用计算方法中，只有塞尔维逊法将波浪增阻直接与绕射力建立起了联系。而切片理论中通常是采用Haskind关系计算总的波浪力，而并不求解绕射势。而三维面元法中绕射问题是直接求解的，同时Haskind关系对于有航速的工况并不适用。这样可以仿照塞尔维逊的做法对绕射增阻进行计算。
考虑浮体的定常力公式，其中二阶力的部分可以写成如下形式［260］：
其中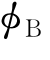
为扰动速度势，它包括了绕射势和辐射势；
和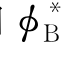
为入射势φ0和扰动势φB的共轭复数。Salvensen［260］通过引入“弱散射假定”φB≪φ0将式（12.101）简化为
通过扰动速度势的分解，移除与辐射势相关的项，并且保留绕射势相关的项，则可以得到绕射增阻的计算公式如下：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
