船舶波浪运动理论中的经典增阻计算方法

1）漂移力法

漂移力法又称为能量与动量法，其基本思想是船体周围有限的计算域内流体的动量和能量的守恒。流场内的速度势被分为入射波、绕射波和由于船舶运动所产生的辐射波。在线性范围内求解流场内的速度势之后，Maruo［256］通过在船体周围建立控制面，并将控制面内流体的动量和绕射辐射势联系起来，进而计算出波浪增阻。Joosen［257］将Maruo的结果进行渐近展开，忽略高阶项和部分耦合项，获得了波浪增阻的表达式：

式中，ωe为遭遇频率，在Joosen的表达式中航速效应仅仅体现在遭遇频率上；B z、Bθ和B zθ分别为垂荡、纵摇以及耦合项的阻尼系数；Z a、θa为垂荡和纵摇的运动幅值。

Joosen认为纵向漂移力主要是由辐射波所产生的，除了短波入射波的情况外，绕射效应对波浪增阻的影响可以忽略。

2）压力积分法

压力积分法是一种非常经典的水动力方法，它最早来源于Havelock［36］的工作，它通过对船体纵向的动压力积分来获得船舶所受到的纵向二阶力。当时对二阶力的计算都是基于切片理论进行的，由于切片理论假定切片之间没有纵向效应的影响，所以很难直接计算出船体纵向受力。Boese［258］在平均纵向力概念的基础上推导出位于x b处的切片所受到的平均力，其表达式为

式中，z x=Z a-x bθa；s和εs分别为x b处切片垂向运动的幅值和相位。通过平均纵向力可以进而计算出波浪增阻，其表达式为

垂向运动所产生的贡献为

这样总的波浪增阻为

3）辐射能量法

辐射能量法最早由Gerritsma和Beukelman［259］（G＆B）提出，其认为波浪增阻所做的功应该与从船体辐射出去的能量相同。在一个遭遇周期内船体辐射的能量E为

式中，b 33是切片的垂荡阻尼系数，可以通过求解二维辐射问题获得，V*z为切片剖面相对于波浪垂向速度，其近似表达式为(www.xing528.com)

式中，ξ*为切片剖面出有效的波形坐标，这个修正是考虑了每个切片处不同的波高所引入的，可以通过下式近似计算：

式中，（y，z）为该切片上的点，y w为该切片的半宽，ξ为未修正的波浪幅值。

位于船后某一位置处辐射波在一个遭遇周期（T e）内所带走的能量应等于船舶阻力平均增值在一个波长内所做的功，即

其中λ为入射波波长。

这样最终的波浪增阻的表达式为

4）塞尔维逊法

船舶在波浪中的阻力增加是一种非线性的二阶力，为了提高计算精度，Salvesen考虑了细长体扰动力和力矩的二阶项后给出了波浪中阻力平均增值的计算方法。其表达式为

式中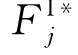，为Froude-Krilov力（即FK力）的共轭复数，为绕射力的共轭复数。FK力的共轭为

绕射力的共轭为

其中，R 7为

在上述表达式中，N 2和N 3为二维剖面边界的外法矢量，C为剖面边界，ψ3为二维垂荡辐射问题的速度势。