船舶波浪运动理论及远场积分法

本节讨论求解作用于船体的二阶平均波浪漂移力的另一种方法，即远场积分法。它的基本出发点是动量守恒定律和能量守恒定律。

设船体无航速地浮于水深无限的水域表面。在空间固定坐标系o 0x 0y 0z 0中，船体湿表面记为S，船体表面的单位内法线矢量记为n=（n 1，n 2，n 3），对流体域而言它是单位外法线。与前述各章的规定一样，空间固定坐标系的o 0z 0轴垂直向上，o 0x 0y 0平面位于未扰静水面上。下面为书写简便起见，略去表示在空间固定坐标系中取值的下标0。

有一列规则波从远方传来，浪向角为β。则场内总的线性速度势（一阶势）为

其中ω为规则波振荡圆频率。这一速度势显然应包括入射波速度势、绕射速度势和辐射速度势。它无疑地应满足拉普拉斯方程和线性化的自由面条件，在物面上满足物面条件：

其中U n为物体表面运动的法向速度；在无限深处所有的扰动消失，即

在水平方向的无限远方，绕射势和辐射势应满足外传波的辐射条件。这些都已在前几章中作了讨论。

在流场中取一流体体积，它由物面S，自由面S F、半径无限大的垂直圆柱面S∞和无限深处某一水平底面S B所围成，并记此流域为τ，S+S F+S∞+S B=Sτ。这样，在体积τ中流体的动量为

式中，为流体质点的速度；ρ为流体密度，动量的时间变化率为

式中，U n为表面Sτ运动的法向速度。根据连续性方程式（2.1）和欧拉方程式（2.2），并应用高斯公式将体积分化成面积分，进而可将上式写成

式中，P为场内压力，由伯努利方程确定，V n=n·V=n·Δ Φ，表示Sτ上流体的法速度。如果只考虑水平方向的力，表征重力势的ρgz项可以去除，因为它对水平方向的动量变化没有贡献。

注意到船体遭受的水动作用力为

而且在物面S上，因物面条件，有V n-U n=0。于是式（12.54）可重新写成

这里i=1，2，即只考虑水平力。

在自由面S F上，p=0，且V n=U n，故上式中自由面S F上的积分不复存在；在底面S B上，V n=0，若底面不动，则U n=0，n i（i=1，2）在水平底面上为零，故S B上的积分亦消失。取半径R为无穷大的垂直圆柱，其控制面是固定的，在此面上V n=V R，U n=0。根据以上讨论，可将上式进而写成

其中V R为流体质点在S∞圆柱面上的径向速度。现取上式在一个完整波浪周期内的时间平均，以各项上加一横线表示之，上式变成

这里我们已经注意到的时间平均为零这一事实，否则的话，将意味着控制体积中动量的无限积累或抽取，而在目前我们考虑的问题中，一个周期内动量应是守恒的。

类似的考虑同样可施于体积τ中的流体动量矩：

其中r=（x，y，z）=（x 1，x 2，x 3）。若我们以广义矢量记V i=（r×V）i-3，n i=（r×n）i-3（i=4，5，6），则可以证明，水平方向的力矩F 6也可同样地表达为式（12.55）［5］。

若引进柱坐标（R，θ，z），且x=R cosθ，y=R sinθ，则式（12.55）还可变形为

上述表达式在无旋流的前提下是精确的。在微幅波假定下，上述表达式可进一步写成明确而便于计算的形式。在以下的推导中将只保留到二阶量。

根据伯努利方程，场内压力为

流体速度在柱坐标系中各分量为

场内总速度势为(www.xing528.com)

式中，ΦI=Re｛φIe-iωt｝为入射波速度势；ΦB=Re｛φBe-iωt｝为扰动速度势，其包括了入射波的绕射影响（绕射势）和船体运动的影响（辐射势）。入射波势可表达为

式中，A为波幅；ω为波浪圆频率；k=ω2／g，为波数；β为浪向角。在柱坐标中，它还可记作

在远场，φB的渐近表达为

其中H（θ）为科钦函数为

由以上φI及φB的远场表达式可以看出，它们在z方向的变化都是指数型的，故而首先在式（12.56）～式（12.58）中对z积分一次，积分的上限为实际波面，即

于是利用伯努利方程：

上述积分过程中，注意到在-∞下限处，或取时间平均后，某项实际上为零，或某项事实上以e-∞形式趋于零，或在之后对θ积分时消去，故只剩下积分上限的贡献。且上式右端第二、三项已关于z=0展开，取至二阶量。同样的做法也可作用于式（12.56）～式（12.58）中的其他项。这样，忽略O（φ3）项，经整理后，二阶平均波浪漂移力或力矩分别可表示为

式中，*号指变量的复数共轭。在推导上式时，已经利用了关系：

和在自由面z=0：

最后，将φI及φB的远场表达式（12.60）和（12.61）代入上面三个表达式，并注意到所有的二次相中，只包含φI乘积的项没有贡献（因为只有入射波时，没有任何漂移力），经整理后可得：

上述表达式中含R的积分可进一步用驻相法（the method of stationary phase）处理。按驻相法，有关系式

这样，式（12.66）～式（12.68）分别可写成

式中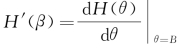，以上三式即为作用于任意船体的水平波浪漂移力和力矩的表达式。

如果说没有外力对船体作净功，例如，船体是完全自由漂浮，则式（12.69）和式（12.70）还可写成更规整的形式。按能量守恒关系［239］：

于是式（12.69）和式（12.70）变为

它们与文献［228，229］的结果是一致的。

对二维柱体，丸尾［228］得出了一个很有意思的结论，那就是作用于二维柱体上的水平方向平均漂移力与来波侧反射波在无穷远处的波幅平方成比例，具体来说有关系式：

这里以|A R|记反射波的远方波幅。当柱体固定不动时，反射波纯粹是对入射波的反射部分；若物体自由漂浮，则反射波中除了入射波的反射部分外，还包含了物体运动向外的辐射波。

上式可由式（12.55）推导而得，其中积分表面S∞应代之以位于x=±∞的两个垂直平面，并且注意到按场内能量守恒，有关系式：

式中，｜A｜为入射波波幅（实际上因入射波是给定的，A总可调整为一实数）；｜A R｜为反射波波幅；｜A T｜为透射波波幅。注意到上述两点后，推导过程即可仿效三维问题进行，感兴趣的读者可自行整理。

式（12.75）说明入射波的能量将完全转化成反射波能量与透射波能量之和。显而易见，除非入射波完全被物体反射，否则反射波波幅总小于入射波波幅，也就是说，当一个二维柱体处于横浪中时，遭受最大的平均水平波浪漂移力为

这在波浪频率很高时达到。高频波的波长很短（当然是相对于物体横向尺度而言的），入射波遇到相对尺度很大的物体将几乎全部反射回去，且这时物体几乎是固定不动的。