船舶在不规则波浪上的运动理论

二阶力表达式（12.16）关于规则波包含了定常二阶力和频率为入射规则波频率两倍的高频二阶力；关于不规则波，则除了有这些力外，还有各成分波频率之差及之和产生的低频分量和高频分量。低频分量即通常所称的慢漂力。本节从不规则波的一般情况出发来阐明这一事实。

不规则入射波通常可记为各种频率的规则波的线性叠加，即

式中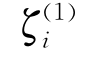，为各规则波的波幅；ωi为该规则波的圆频率；εi为相位角。

式（12.16）中最后一项为以此为例进行考察。

按线性理论，船体水线上某点的一阶相对波幅为

式中，为相对波幅对来波波幅的比例系数（对某一i分量）。将上式代入式（12.27），经整理可得到

其中

至于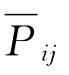和，只要将上面两式中εri-εrj改作εri+εrj即得；εri，εrj分别为相对波幅i分量或j分量对来波波幅相应分量的相位差。上式中P ij，Q ij，和都是与时间无关的。(www.xing528.com)

类似地，对二阶力的各分量进行分析，它们均可写成式（12.28）的形式，当然它们的总和也是这一形式。于是，认为式（12.28）即是二阶波浪力的一般表达式，但P ij、Q ij、和除了有形如式（12.29）的表达外，还有其他各二阶力分量的相应表达，它们的和即为总的二阶波浪力一般表达式中的P ij，Qij，和。与入射波的平方，即

相比较，易知，P ij，Q ij及，均为平方阶的传递函数（quadratic transfer function），P ij联系着与来波平方的低频部分同相的二阶波浪力，Q ij联系着与之相位差π／2的二阶波浪力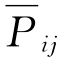，与意义类似，只不过它们是与高频部分相应的。

由式（12.28）中可知，二阶波浪力中既有差频（ωi-ωj）项，又有和频（ωi+ωj）项。当ωi与ωj相近时，（ωi-ωj）可以很小，即振荡频率很低，通常所谓的缓变波浪漂移力或慢漂力指的就是这部分低频力。和频项中，除频率为ωi+ωj外，还有各分量自身的倍频项2ωi或2ωj。除此之外，式（12.28）中还包括了平均波浪漂移力。事实上，若i=j时，平均波浪漂移力为

它是一个定常力，不随时间变化，若来波是单-频率的规则波，则式（12.28）变成

其中即为P ii，；ε在这里指来波相位，上式中只包含定常力和倍频力。

需要指出的是，如果只求解定常波浪漂移力（无论是否处于规则波中），则只需要把一阶势和一阶运动求出即可，因为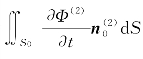中不包含定常分量，这一点将在下一节继续讨论。

如果已知二阶传递函数P ij，Q ij，那么根据给定的波浪谱就可以求得定常二阶力和缓变二阶波浪漂移力［232］。这里不再讨论。