波浪中相邻浮体的耦合运动时域方程

本节介绍的多浮体耦合运动时域方程，其部分系数可以从频域转换得到。例如，可将浮体在波浪中耦合运动的频域水动力系数［见式（11.30）］转换为时域方程中的时延函数等，而作用在每个船体上的静回复力的表达式与单浮体情况相同。

从运动学角度来看，此处给出的多浮体之间没有任何刚性或柔性的连接，因此波浪中多浮体各自的运动是相互独立的，某浮体的运动并不会直接改变相邻另一浮体的运动状态。每个浮体的运动有6个模态，则N个浮体组成的系统共有6N个自由度的方程，整理可得第l个浮体的运动方程为

式中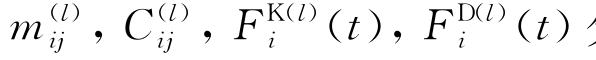，分别是第l个浮体的广义质量、静回复力系数以及入射波和绕射波的波浪激励力，x为运动位移。

由上面的方程可以看出，第v个浮体的运动之所以会对第l个浮体的运动造成影响，是因为第l个浮体的运动方程的左端含有与第v个浮体运动相关的项。若浮体为两个，可依次令上标l，v等于1和2，则浮体运动方程可具体化为(www.xing528.com)

显然单独求解一个浮体的运动方程是不可能的，只能将它们联立求解，才能得到浮体的运动时历。将浮体1和浮体2的运动方程联立，为表达明晰起见，下面将方程改写为矩阵形式，如对应浮体1的时域运动方程为

其中系数矩阵［M］，［μ］，［C］，［K］均为6×6矩阵，其元素的下标取决于运动模态；［K］矩阵元素的具体表达式如下：

上述多浮体耦合运动时域可采用四阶龙格-库塔法求解运动方程组，同时可以得到浮体1和浮体2各自的6模态摇荡位移。这是基于势流理论的时域运动方程，实际应用中仍可以类似公式［见式（11.22）］增加黏性力F vis对横摇阻尼进行修正，增加外力F ext来确定浮体间其他相互作用力（如两船补给作业时的外力），实践证明这些方法描述两船耦合运动是有效的。