参数横摇多水平预报方法

以下将给出船舶参数横摇预报的几个不同水平层次的理论预报方法，来帮助读者逐步理解船舶参数横摇发生的机理，了解应用于工程实践的基础。

1）零级水平——发生预报

在遭遇频率为ωe的入射波作用下，假设初稳性高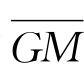简谐变化，且阻尼为线性模型，单自由度横摇运动方程又可表示成

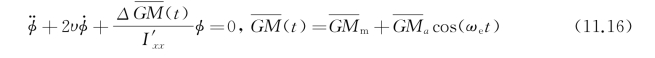
式中，Δ为排水量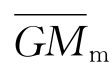是横稳性高的平均值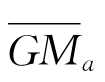是横稳性高随波浪变化的幅值。令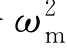=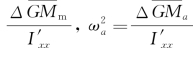，则式（11.16）转化成为

引入无因次化时间τ=ωet，则式（11.17）变形为

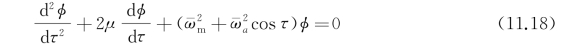
其中μ=υ／ωe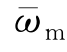，=ωm／ωe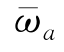，=ωa／ωe，令φ（τ）=φa（τ）·exp（-μτ），式（11.18）转化成标准的Mathieu方程，即

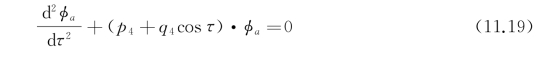
式中，p 4=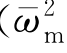（-μ2）；q 4=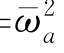。p 4反映了横摇固有频率与遭遇频率之比；q 4反映了横稳性高随波浪变化而变化的程度，是衡量参数激励幅度的一个指标。以p 4为横坐标，q 4为纵坐标，绘成Ince-Strutt图谱，如图11.5所示。其中，阴影区域为Mathieu方程解不稳定区域。第一个非稳定区域标记为1，与p 4轴相交于点p 4=0.25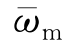，=0.5，即激励频率为固有横摇频率的两倍。这个区域内产生的共振为主参数共振。第二个非稳定区域标记为2，与p 4轴相交于点p 4=1，即激励频率等于固有横摇频率，在这个区域内产生的共振为基本参数共振。基本参数共振区域对应的频率范围小于主共振区域的范围。

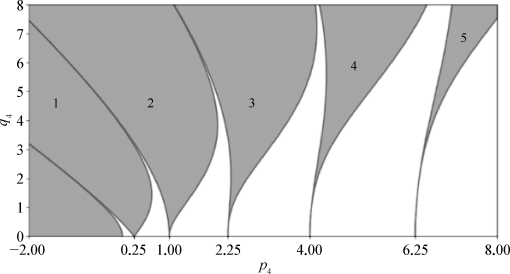
图11.5　InceStrutt图谱

2）一级水平——变化GM／GZ法

变化GM／GZ法是一种简化的方法，它是在考虑垂荡和纵摇运动的前提下模拟横摇运动。很多情况下，横摇与垂荡和纵摇的耦合并不十分明显。那么就可以先计算垂荡和纵摇运动，再求解横摇运动方程。虽然横荡和艏摇会与横摇运动耦合，但是这种耦合效应很弱，并且通常认为参数横摇与其他自由度的耦合并不是很明显。因此，单自由度横摇运动方程就可以写成

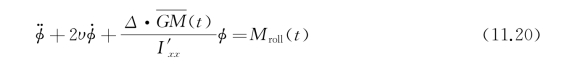(www.xing528.com)

式中，I′xx为船体本身横摇惯性矩和附加惯性矩之和，右端横摇波浪力M roll（t）包括线性绕射波浪力以及非线性的傅汝德　克雷洛夫力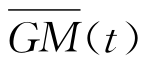，为非线性回复力。运用切片法或者其他更精确的方法得到每一时刻的湿表面，通过瞬时湿表面压力积分获得非线性力。一种更为简单的方法是假设初稳性高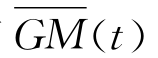简谐变化，再利用傅里叶级数展开：

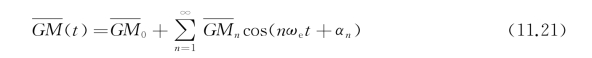
其中的常数项和级数展开第一项是主要成分。

3）二级水平——脉冲响应函数法

模拟非线性横摇运动的方法有很多种，其中基于弱非线性假设的脉冲响应函数法是最有效率的方法之一。这种方法又称为混杂法，它考虑了非线性傅汝德-克雷洛夫力和非线性回复力，但是辐射力和绕射力仍然保持线性。近年来，混杂法被广泛应用于耐波性分析中。

参照第10章式（10.91），考虑水动力系数，包括无穷频率对应的横摇附加质量μ44（∞）和时延函数R（τ），运动方程可以表达成如下形式：

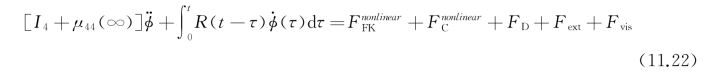
右端力项包括非线性傅汝德-克雷洛夫力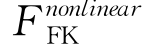、非线性回复力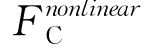、外力F ext和黏性力F vis，绕射力可以从线性频域结果转换而来。

由于横摇角的幅值对黏性效应十分敏感，所以横摇激励力还包括黏性力。黏性力可以通过等效线性阻尼系数与速度的乘积获得：

通常等效线性阻尼系数b equi_vis可选取为临界阻尼的5%～10%。

4）三级水平——时域面元法

根据第10章的时域理论方法，带有实时自由面处理的三维时域面元法，包括简单格林函数法和区域分割的混合格林函数法，可以实现求解参数横摇发生时瞬时湿表面变化引起的非线性回复力，此方法可靠实用，对自由面模拟要求较高。时域运动模拟、自由面的处理和参数横摇等相关文献可参见陈曦［216］、Kim［89］等的研究。

该方法中速度势被分解为三个部分：基本势、入射势以及扰动势，自由面条件以及其他边界条件也可线性化简化。船舶表面和自由面被离散成有限个面元，应用格林第二公式适当推导出的边界积分方程，求解就可获得瞬时波面升高和物面速度势，在船体表面进行压力积分就可获得水动力。与脉冲响应函数法相似，面元法中仍然保持辐射力和绕射力为线性，压力积分在平均湿表面进行，而傅汝德-克雷洛夫力和回复力均在瞬时湿表面通过压力积分获得。

5）四级水平——CFD模拟法

尽管解决波浪和耐波性问题多以势流为主，但关于其应用在黏性和非线性影响较大的问题研究方面有明显的不足。CFD模拟基本可以参照物理水池实验的方法进行。鉴于本书主要以势流理论方法为主，此处不再过多展开。其实现方法和内容可参见相关文献，如蒋银等［217］建立了基于RANS方法的船舶运动虚拟试验与测试，提出为有效发挥CFD优势直接进行时域模拟船舶参数横摇，对船体遭遇波浪时的运动初始阶段，可以采用适当的初始扰动激励方式。CFD方法考虑了流体的黏性，对自由液面进行实时捕捉，能根据瞬时湿表面积计算回复力，该方法不仅能模拟参数横摇的发生，也能模拟大幅度参数横摇后非线性现象的发展，对带附体的复杂船型的适应性、计算结果的精度、物理机制认识等方面都均有良好的效果。