船舶波浪上运动的理论

高速细长体理论最早由Chapman［27］提出，而后由Faltinsen和Zhao［28］，Takaki等［211］扩展到船舶耐波性领域的预报。该理论针对快速船型的几何形状的细长体特性，对船体周围的流场保留了二维假定，这和普通切片法的假定是一致的，不同之处在于该理论的定解条件中保留了三维线性自由面条件，考虑了流场沿船长方向上的变化。从两者自由面条件的比较中可以看到：普通的切片法理论考虑了沿船长方向上平行传播的波系，而高速细长体理论则保留了沿纵向传播的散波系，这符合航速较高时纵向兴波的实际规律；在航速较高时，高速细长体理论假设在船艏处非定常扰动势为零，这条假设要求船舶的航速要足够高，对于航速不太高的肥大性船型，这条假设是不能成立的。故高速细长体理论适合于高航速下的船舶耐波性的预报。该方法较普通切片法的可取之处是考虑了自由面的三维流场效应，这是对常规切片法的一个拓展。高速细长体理论求解的流场是二维的，而自由面条件是三维的，因此又称为2⅟²D理论（即二维半理论）。

目前很多学者研究了二维半理论在高速船舶水动力预报上的应用。各种方法的不同之处在于如何处理自由面条件和远方辐射条件。有些学者采用了简单格林函数的方法来求解高速细长体理论的扰动势，自由面的三维边界条件通过差分方法从艏部到艉部步进计算。该求解方法的缺点是水动力计算的精度不易保证。

二维半理论是基于切片理论发展的，和切片理论中采用的坐标系、细长体假定等相同，这里不再赘述，但二维速度势满足的自由面条件与三维的理论一致，即应用第8章中式（8.2），而非式（8.3）。

另外假设船舶航行的速度足够高，在船舶的艏部以前区域（记为x＞x f）没有非定常流场的扰动，即船前无兴波，要求Brard数。根据此假设要求：

其中x f是船艏纵向坐标。

将空间与时间互换，作变换x=x f-U 0t，对于每一个横剖面，其纵向坐标也决定了时间t的值。

不失一般性，下面仅以辐射势说明二维半理论的定解问题。引进函数：

根据φj的定解条件可以确定ψj的定解条件。在每个横剖面域内，ψj满足Laplace方程，根据下面的求导关系式：

可得ψj在自由面上应满足的条件为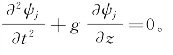

综上可得(www.xing528.com)

该定解问题中不同“时刻t”相应于不同的横剖面位置，Laplace方程与不同时刻t有关，相当于考虑瞬时湿表面的非线性时域问题，自由面条件还是线性的。此定解问题一般采用时间步进求解，相当于初始为零航速二维柱体振荡，随时间步进，湿剖面周界相对应于船体横剖面从艏到艉变化，各横剖面流场解通过步进求解得到。国外学者们采用简单格林函数在时域内步进求解该定解问题。由于该方法需要利用数值表达流场辐射条件和自由面条件，而数值处理常常会带来误差和计算失稳问题。段文洋［33］提出用二维时域格林函数构造分布源边界积分方程来求解ψj（t，y，z）及其横剖面内空间导数，提高了二维半理论解决高速船舶水动力问题的效率和稳定性。二维时域格林函数与三维时域格林函数形式类似，即

其中反映自由面记忆效应的记忆项：

类似于三维时域方法，从分析平均自由面上的积分出发，可得到

式中，α为域内场点处的空间角，点在域内则为2π，在边界上则为π；P 1［y 1（ξ），0］，P 2［y 2（ξ），0］为横剖面周线和y轴的两个交点。

通过数值方法求出ψj，相应模态的辐射力可表达为

其中ξja为j模态运动幅值。

类似的方法可以获得绕射波浪力和入射波力，即

将辐射力、绕射力和入射波力代入运动方程（7.35），则可以得到二维半理论下船舶运动频域方程。