混合格林函数法通过将流场划分为内域和外域,分别引入Rankine源和自由面格林函数并结合控制面上的连续条件进行初边值问题的求解,实现了兼具两者优点的目标。文献[97]关于圆柱形平台和S175船进行数值计算和验证,给出了时延函数、波浪力幅值和运动响应结果,并与频域方法和试验数据作了对比。数值结果和试验数据在计算频率范围内吻合良好,表明混合格林函数方法正确可靠,对无航速和有航速水动力问题均适用,能有效解决外飘船型的发散问题。同时其作者针对Wigley型船进行了一系列数值计算,研究了时间步长、自由面和控制面面元的划分对计算结果的影响。选取合适的参数对LNG船在不同浪向中的运动响应进行了计算。数值计算结果和试验数据吻合良好,能够对大外飘浮体在斜浪中的运动进行时域模拟,并为研究其他更复杂的耐波性问题奠定了基础。
图10.6为混合格林函数法计算S175船所用的网格。
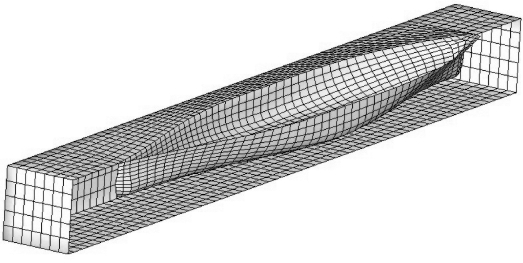
图10.6 混合格林函数法计算S175船所用的网格
在弱散射假定下,即时域船体运动方程中的辐射波浪力和绕射波浪力由线性理论计算获得,入射波波浪力和静水恢复力利用瞬时湿表面的计算获得,可进一步进行弱非线性时域运动预报。文献[97]对Wigley型船和S175船在波浪中的运动进行了一系列数值模拟。船体运动响应的时历曲线与线性方法得出的曲线形状基本一致,这里不再单独给出。对Wigley型船和S175船在不同频率规则波中的运动进行一系列计算后,通过傅里叶变换就可以得到其运动响应幅值算子(RAO)。图10.7和图10.8分别给出了Fr=0.2和0.3时迎浪航行的Wigley型船的垂荡与纵摇RAO,其中实线为非线性方法的结果(non-linear),虚线为线性方法的结果(linear),矩形点为Journée[209]的模型试验结果。
图10.9~图10.11分别给出了Fr=0.275,浪向角β为180°、150°、120°和90°时S175船的垂荡、横摇与纵摇RAO。其中实线为非线性方法的结果(non-linear),虚线为线性方法的结果(linear),矩形点为第15届ITTC会议[210]给出的模型试验值。
由上述一系列图可以看出,尽管线性方法的计算结果已经令人满意,但弱非线性方法给出的结果仍有改善,其与试验值均吻合程度更好一些。相对垂荡模态来说,纵摇和横摇模态的运动预报有较明显的改善,这证明了非线性入射波波浪力的差异确实带来了积极的影响。此外相对Wigley型船而言,S175船的预报结果改善得更为明显,这是因为后者的外飘船型导致瞬时湿表面和平均湿表面之间的差异较大,这种情况下非线性方法计算精度更高。
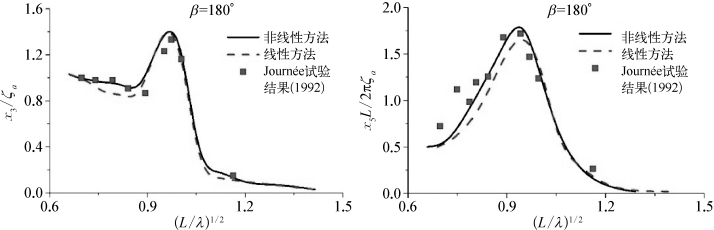
图10.7 Wigley型船迎浪时的垂荡和纵摇RAO(Fr=0.2)(https://www.xing528.com)
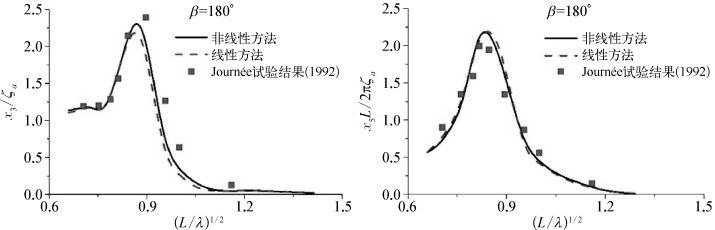
图10.8 Wigley型船迎浪时的垂荡和纵摇RAO(Fr=0.3)
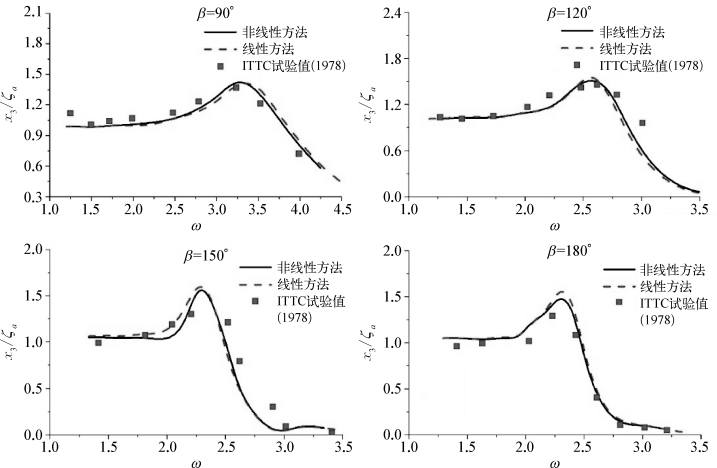
图10.9 S175船在不同浪向下的垂荡RAO(Fr=0.275)
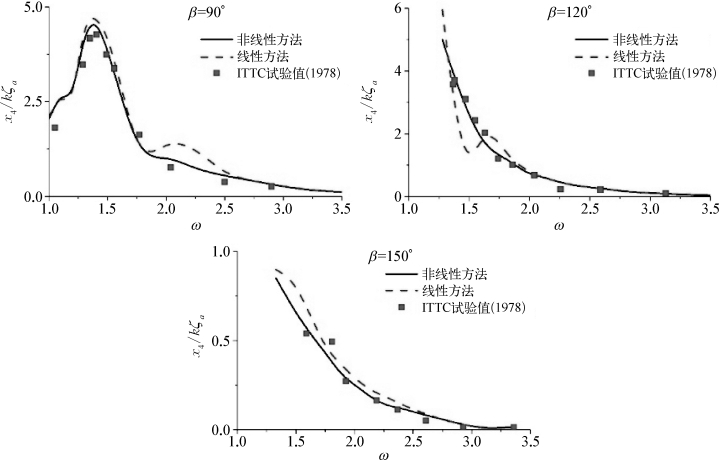
图10.10 S175船在不同浪向下的横摇RAO(Fr=0.275)
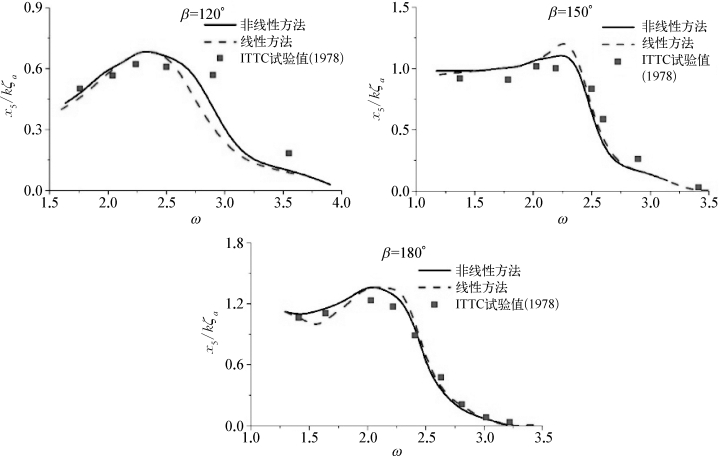
图10.11 S175船在不同浪向下的纵摇RAO(Fr=0.275)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




