采用面元法时域分析求解水动力问题时，格林函数的计算涉及多重积分，在每个时间步上都需要建立和求解积分方程，计算量极为庞大。国内许多学者也正在开展时域问题和时域格林函数的相关研究，黄德波［199］、叶恒奎［200］、詹成胜［201］等分别对三维时域无限水深格林函数进行了计算研究，韩凌［202］、滕斌［203］等针对三维时域有限水深函数的计算及其在波浪和物体相互作用模拟上的应用进行了研究。近年来，尽管计算机技术有了飞速的发展，三维时域格林函数的计算仍然是个难题，因此如何精确而又快速地计算时域格林函数及其导数是求解船舶水动力问题的关键。
三维时域格林函数是个无穷积分，被积函数具有高频振荡和增幅的特性，因此对于该函数的计算非常困难。对深水格林函数计算处理，早期的方法是级数展开，配合渐近式的算法，如Newman［74，149］、Liapis［204］和Beck［72］等，将其应用在水动力学问题的求解时，需要较长的计算时间；后来Ferrant［205］，Magee［206］，黄德波［199］等采用了适合在PC机上实现的节点值制表和节点间插值的方法。对制表节点计算时，把被积函数的振荡部分按时间大小分区域，小时间区域上采用级数展开，大时间区域上使用渐近式的算法，应用于船舶水动力问题计算时按双变量进行查表插值。关于这种算法，大小区域的划分界线很不容易掌握，虽然计算时间大为减少，但精度有所降低，而且格林函数高频振荡，节点不够密的话，节点间格林函数的插值精度很难保证。Clement［75］，段文洋等［207］分别采用了不同的方法推导出时域格林函数所满足的常微分方程式，但目前尚无相关应用的文献。Clement在文献［75］中提出用常微分方程代替无限积分的运算，不过大时间区域上的格林函数计算精度因常微分方程的计算步长的选取而显得尤为敏感，采用较小时间步长求解常微分方程时，较多时间步后的数值误差很难界定。
朱仁传等采用新的方法推导了时域格林函数所满足的常微分方程式，结合常微分方程易于计算的特点，提出了一种新的实用计算方法，即对表格节点的计算采用级数展开和渐近表达以保证其精度，应用于水动力问题求解时，时间方向上的插值采用直接求解常微分方程，其结合了制表方法的简洁快速和微分方程的精确，同时保证了计算的效率和精度。数值计算表明，该方法能有效地计算三维深水时域格林函数，适用于三维时域船舶水动力势流问题的求解。
时域格林函数瞬时效应部分的计算较为简单，计算困难主要来自记忆效应部分，对应的波动效应部分可表达为
记流场中的场点、源点分别为p（x，y，z）、q（ξ，η，ζ），那么式中变量Z=z+ζ，r=
，r是场点与源点水平方向的距离。令
，并引入变量
，则时域格林函数的波动部分可写成
其中
式中，μ、τ为参数，且0≤μ≤1。由此可以看出时域格林函数可归结为含两个参数的函数。函数F对时间τ的各阶导数所满足的四阶常微分方程如下：
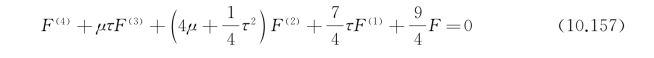(www.xing528.com)
根据零阶Bessel函数和一阶Bessel函数所满足的方程，可进一步推导出格林函数波动部分在水平和垂直方向上的导数分别应该满足的常微分方程：
将式（10.157）写成一阶线性微分方程组的形式，则有
其中Y=｛F，F（1），F（2），F（3）｝T
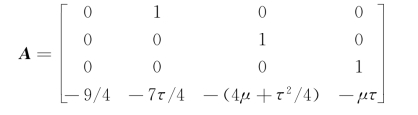
假定有了τ0时刻的Y值，直接采用数值计算方法求解方程组就可推算出τ0以后时刻的格林函数值。文献［97］通过求解常微分方程法计算了时域格林函数及其导数，图10.3为应用该方法计算得到的时域格林函数变化曲线。
时间方向上节点间的格林函数波动部分的计算，利用求解常微分方程的方法（四阶矩阵运算），计算速度非常快。而离散求解微分方程，其精度主要来自离散格式和时间步长，因此一旦选定微分方程的离散求解格式后，采用适当小的时间步长就能保证节点间格林函数值的精度。研究表明以四阶龙格库塔作为微分方程的离散求解格式，当采取0.001的时间步长计算时，其结果与直接使用渐近展开方法计算的结果误差接近，都在10-7次以内。
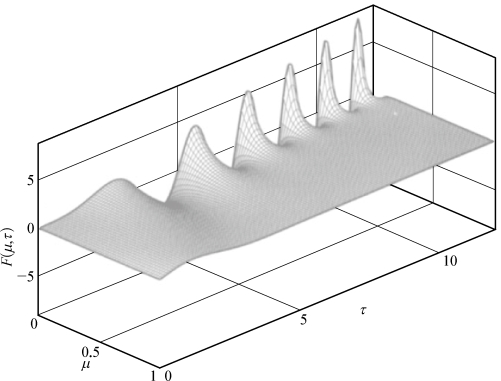
图10.3 μ=0时的时域格林函数的波动部分
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
