船舶波浪上运动：简单格林函数法结果

Rankine源方法也称简单格林函数法，该方法用基本解ln r（二维）或1／r（三维）作为格林函数，不加边界条件修正项，因此奇点分布需要遍布整个计算域。该方法的优点是形式简单，易于实现，避免了计算复杂自由面格林函数，自由面和船体的非线性效应也便于计入。然而相比于自由面格林函数法只需在物面分布源偶，Rankine方法离散的网格数量巨大，并且存在数值稳定性的问题。

早期的Rankine源方法应用于求解船舶兴波问题，Dawson［186］首先在Hess和Smith无界绕流数值计算的基础上采用Rankine源进一步计算船舶在静水中航行产生的兴波波动势。Yeung［187］将Rankine源法应用于任意三维物体在静水中的强迫振荡计算，计算过程中将远场辐射条件转换到有限域处理，他还给出了无限水深下计算的改进方法。贺五洲和戴遗山［188，189］也采用该方法求解船体的三维频域水动力系数，着重讨论了计算中对辐射条件的处理，提出了流体域匹配的方法，采用有限的圆柱控制面将流域分为内外两部分，外域采用速度势特征函数展开式表达，内域用Rankine源计算，最后进行匹配。Nako和Sclavounos［57］将该方法应用于三维有航速船体在波浪中运动的数值模拟中，通过对不同航速下Wigley和60系列船型计算得到的水动力系数、波浪激励力和运动响应结果与实验对比，验证了该方法可以有效处理航速产生的项，证明三维方法的计算精度高于二维理论。

应用简单格林函数法，一般有

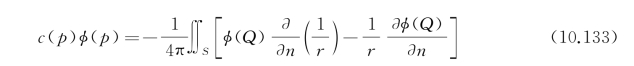
式中，c（p）为固体角；边界面S=S 0+S F+S B+S R，包括了所有的流体边界面：物体平均湿表面S 0、自由面S F（z=0上）、池底S B和半径R无限大的垂直圆柱面S R所围成的流域。

各边界条件可参照式（5.11），得在物面S 0上是已知的；若用线性自由面条件，S F上有，其中；池底；辐射面S R上有

实际计算中自由面需要截断，数值实验的结果表明随着辐射区的宽度不同会得到不同的速度势，即S R大小的选择直接影响了计算结果。分析可知：兴波问题和Brard数τ大于0.25时物体摇荡兴波问题［55，190］，在自由面条件中对流项起到主要作用，外边界上的反射对内域解的影响不是十分敏感；对于无航速或τ很小的问题，对流作用很小，外边界上任何反射对内域解将产生很大的影响。因此边界上必须采用数值黏性的方法，使外传波通过黏性层后被吸收完全，没有反射波，如文献［86］的辐射边界条件是通过阻尼系数μ的形式施加于自由面控制方程中，即

μ定义为

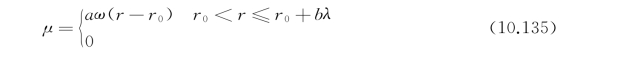
式中，r为节点到计算域中心的距离；r 0为阻尼区域的起始位置；a和b是系数。(www.xing528.com)

在边界上采用特征函数展开，让辐射波外传通过，如图10.1所示，若在边界及以外处是平底，水深H，则可假定辐射面上速度势可表达为

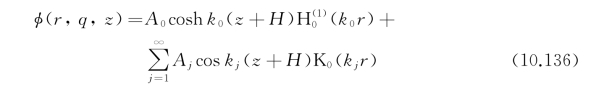
式中，（·）和K0（·）分别是零阶汉克尔函数和零阶第二类修正贝塞尔函数；k 0和k j分别是方程ω2=gk tan k H和-ω2=gk jtan k jH的根；A 0和A j是待定系数。最后通过边界面匹配，配置点的速度势和特征函数展开式中的待定系数可一起求解获得。

以上所述均为频域理论，在时域应用方面，计算量会剧增，Rankine源法不仅要解决辐射条件的处理，还存在时域计算的稳定性、计算效率以及在非线性方面的应用问题。

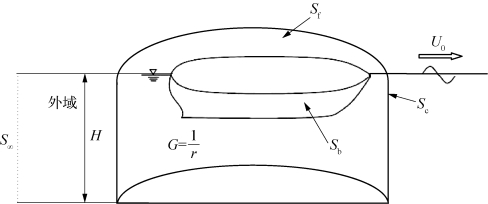
图10.1　内外域匹配法

关于辐射条件的处理，Ferrant［86］应用时域Rankine源研究波浪和固定或自由漂浮结构的线性作用问题时，采用在自由面上增加阻尼消波区域的方法来满足辐射条件，此做法的优点是不需要在远方划分控制面网格，但是阻尼层参数的选取需要通过大量计算来确定。Isaacson和Joseph等［191］在研究三维圆柱的二阶波浪辐射问题中采用了Sommerfeld型辐射条件，该做法需要事先知道远场控制面处透射波波速，对于线性问题和基于摄动展开的二阶非线性问题，波浪参数已经确定，因此其计算中可以采用该方法。Zhang［192］在应用时域Rankine源法计算二阶斯托克斯波和海洋结构物的非线性相互作用问题时还采用了Orlanski型辐射条件［192］及其改进方法，该类型辐射条件需要划分两组控制面，透射波速通过计算两组控制面间的法向速度得到，计算量庞大，改进型的方法不需要设置两组控制面，透射波速由自由面最外沿处的差分得到，然而不论何种方法，差分计算均会产生稳定性问题，该方法的优点是不需要事先知道透射波速度，因而在全非线性模拟中可以应用。

时域Rankine的另一个核心问题当浮体具有航速或在某些特定短波下，时域模拟会发散，现在流行的处理方法是在自由面与浮体的交线上采用低通滤波技术（low-pass filter）。Buchmann［193］将三点低通滤波技术用于线性边界元法中。Shao［194］采用同样的方法研究了低航速下的浮体和波浪非线性作用问题，并且考察了不同滤波强度下的计算结果，研究发现，在一定范围内不同滤波强度不会对计算结果产生影响。

频域计算通常只需做20～40个不同的频率，而时域计算要完成成百上千个时间步，计算量大幅增加。为提高计算效率，有研究者对格林函数基本解1／r进行多级展开（FMM），当源点靠近场点时采用传统方法计算影响系数，同时对远离源点的大量场点进行聚合、转移和配置来计算，大大缩短了构造边界积分方程系数矩阵的计算时间，提高了时域Rankine源法的工程适用性，这一改进方法也称为快速多级边界元法（FMBEM）。Bai和Taylor［195］、Shao［194］还采用分解流域法来提高Rankine源方法的计算效率。除此之外，采用高效的迭代算法来求解边界积分方程也能显著的提升计算效率，例如，很多学者都采用了GMRES求解器。

Isaacson和Joseph等［191］、Zhang［192］、Shao［194］基于对速度势和自由面升高的二阶摄动展开，采用Rankine源法研究了流体和浮体的非线性相互作用。宁德志［196］、Bai和Taylor［195］、Ning和Teng等［197］将该方法用于完全非线性数值水槽的时域模拟中，自由面条件为完全非线性，计算基于混合的Euler-Lagrange方法，在每一时间步求解Euler格式描述的边界积分方程，数值计算中格林函数依然选用基本解，移动边界通过Lagrange格式在各时间步之间更新，自由面上速度势和自由面升高的导数，结合高阶面元法的坐标变换关系直接求解。