船舶在波浪上的运动理论：解决有航速问题

假设船舶在波浪中以航速U沿x轴正方向前进，在波浪作用下做六自由度的摇荡运动，并假定船舶的摇荡运动是微幅的。与有航速频域问题一样，有航速船舶的辐射及绕射问题中，取随船前进的平动坐标系作为参考坐标系，仍然把场内速度势分解成物体振荡的辐射势ΦR、入射波速度势ΦI和绕射速度势ΦD的线性叠加。

辐射势ΦR满足的初边值问题与10.3节中的略有不同，由式（4.57）知，线性物面条件可写成

假定船体移动的定常兴波为小量，则m j项具体表达参考式（4.58）。自由面条件变为

由前文可知，在无航速工况下，有

在物面上的场点处：

上式可以改写成

两端对时间积分，则

对τ=0时刻使用格林第二公式：

将式（10.103）代入式（10.102），并结合自由面上格林函数初始条件0）可得：

对式（10.104）右端最后一项使用自由面边界条件式（10.98），并参照本章附录中变化率公式：

式中，wl是船体湿表面与静水面的交线，N是平面曲线wl的单位法线向量，指向船体内部，V N是周线wl沿法向N的法向运动速度。

将式（10.105）代入式（10.104），得到大地坐标系下扰动势的边界积分方程：

如果速度为0，则其与10.3节的表达含义相同。

下面考虑参考坐标系扰动势的边界积分方程表达。在有航速时，大地坐标系下时刻τ的微分在参考坐标系下为。在现在情形下，速度包含船速U和六自由度摇荡速度，而由于摇荡速度是无穷小，只保留船速即可，则

将以上关系代入式（10.106）可得有航速时参考坐标系下扰动势的边界积分方程：

同样采用脉冲响应方法来进行求解，由于航速的出现，可将式（10.59）改写成如下形式：

其中δ（t）是Dirac函数，H（t）是阶跃函数。它们分别满足如下的定解条件：(www.xing528.com)

和

绕射势的情况相对简单，只需将自由面条件用下式替换，其余初边值条件不变：

此外，公式中的波浪自然频率ω也需要用遭遇频率ωe替换。

辐射和绕射势定解问题的求解方法和10.3节相同，此处不再赘述。

有航速情况下流场中动压力和作用于船体的流体动力的计算方法与无航速的也基本相同，这里只列出由于出现航速而需要改变的公式。

根据线性伯努利方程，辐射力可表达如下：

由式（10.108）可得

将上式代入（10.113）可得

其中

波浪力F Wi的表达式变为

作用在物体上第i（i=1，2，…，6）运动模态的绕射力的表达式变为

绕射力的脉冲响应函数如下：

则压力计算的脉冲响应函数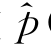（P，t）表达式变为

将有航速情况下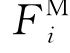的表达式代入式（10.90）并稍加整理，运动微分方程最终可写成

显然，由于船速的出现，时域运动方程左端多出b ij和c ij两项。