船舶绕射问题的线性时域解

绕射问题中不考虑物体的摇荡运动，对于无航速浮体的绕射问题来说，只计入入射波与浮体之间的流体动力干扰。根据10.1节内容，绕射势用ΦD（x，y，z；t）表示，其定解问题如下：

通过对比绕射问题和辐射问题的定解条件，不难发现它们之间的主要区别在于物面条件的表达不同。绕射问题的物面条件只跟入射势ΦI有关，而ΦI是作为已知项来处理的，所以总体来说，绕射势的求解要比辐射势简单。绕射势的边界积分方程表达式与辐射势的相似，即

对此式两端求时间导数，并积分代入初始条件和绕射问题的物面条件，可得

King和Beck［78］根据对于时域线性系统的脉冲响应函数与任意系统输入对应的输出之间的关系式，得到对应于任意入射波的波速变换关系式。假定入射波波面升高为ζ（t），脉冲响应函数为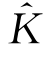（p，t），那么

式中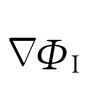，（P，t）表示入射波波面升高为ζ（t）时，对应的系统输出即入射波波速。

对于入射波为规则波的情形，即ζ（t）=eiωt，那么单位入射波势可以用下式表示：

式中，g为重力加速度；ω为波浪自然频率；β为浪向角；k=ω2／g；α=x cosβ+y sinβ。

根据式（10.65），可以得出如下的规则入射波波速的表达式：

把式（10.66）代入式（10.64），根据傅里叶逆变换，并保证脉冲响应函数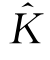（p，t）为实数，可以得到

其中Re｛｝表示取实部。

对于波浪力的重要组成部分绕射力的求解是建立在绕射势求解的基础上的。

下面就如何应用脉冲响应函数计算绕射力作进一步分析。绕射势可用如下的卷积积分表达：(www.xing528.com)

根据绕射定解问题，绕射势的物面条件可以表达为

把式（10.64）代入上式可得

由式（10.68）和式（10.70）可得

至于（P，t）的求解，数值计算的方法和ΦD（P，t）的求解是一样的，唯一不同的是对应的物面条件，即式（10.50）和式（10.52）。

在频域计算中，曾引入哈斯金特关系，只要物体运动的辐射势已经求得，不必求绕射势即可得到波浪绕射力；在时域计算中，同样可以利用类似的关系式。

设辐射势已经求得，那么根据式（10.55）可以得到φj（P，t）。现考虑由物面S 0、自由面S F、无限深处底面S B及半径R无穷大的垂直圆柱面S∞所围成的流体域。在域中φj（P，t）和都是调和函数，按格林公式，可有

由φj和ΦD满足的辐射条件，当R→∞时，在S∞面上的积分将消失。另外，利用它们满足的自由面条件，在S F面上的积分可重新表达成

将其代入式（10.72），并将该式对τ由0至t积分，得

已知，当P∈S F时，，故上式中右端第二项积分消失。考虑到这一事实，现在再将式（10.73）对t求导，并注意到等在该瞬时τ或0都是个确定值而不是t的函数，可得

在物面S 0的积分中，可以用来代替，在S F上和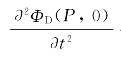作为初始值应是已知的，因而，按式（10.63），波浪力（包括入射波和绕射波）最终可表达为

上式即可看作时域中类似哈斯金特关系的一个表达式，利用此式可在波浪力计算中避免复杂的绕射势计算。