时域问题和格林函数解

设船体在水面上做任意形式的摇荡运动，运动可以由入射波及其在船体上的绕射影响所引起。流体或船体的初始位置和速度是已知的。在讨论中，我们将认为这些摇荡运动仍然是围绕其平衡位置的微幅运动，运动位移或速度的平均值为零。这样，在线性化假定下，物面条件被认为在船体表面的平均位置上得到满足，自由面条件则在静水面上满足。为简单起见，在此我们暂时先不考虑有航速的情况。

如第2章所述，我们选空间固定坐标系o 0x 0y 0z 0和固结于船体的动坐标系oxyz以描述船体的运动位置和姿态。空间固定坐标系的o 0z 0轴铅直向上，o 0x 0y 0平面位于未扰静水面上。当船体没有摇荡运动时，动坐标系与固定坐标系重合。如前述章节中所指出的，当船体运动为小量时，由于坐标系差别而引起的误差将是高阶小量。因此，在一阶近似的线性理论中对此可不做严格的区分。这里，约定在空间固定坐标系中考虑问题，并为叙述简洁起见，将空间变量（x 0，y 0，z 0）简记作（x，y，z）。

显然，场内的流体运动仍然可以用速度势Φ（P，t）来描述，其中P指流场中任一空间点，它的位置坐标为（x，y，z），速度势Φ（P，t）应该满足：

式中，S 0为船体的平均浸湿表面；V n为S 0上点运动的法向速度；（t）为j模态的运动速度；n j为物面单位法线矢量在j向的投影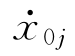；（t）和n j都是在广义意义上理解的。除了上述方程和条件外，速度势Φ（P，t）还应满足辐射条件和初始条件。

现在的辐射条件与以前所述有所不同。若认为运动是由t=0时开始，则对于有限的时间t，扰动的影响还没传到无穷远处，那里的流体仍然是静止的，或者只有入射波的影响。如果我们仍然把场内速度势分解成物体振荡的辐射势ΦR、入射波速度势ΦI和绕射速度势ΦD的线性叠加，即

那么，扰动影响部分ΦD和ΦR满足的辐射条件是：

它们的物面条件则分别为

初始条件应对所有的流体边界给出。显然对物面来说，位置是已知的，物面上流体速度的初始条件可简单地令式（10.4）中t=0得到。在自由面上，初始条件则应为

和

式中，P∈S F，S F是静水面，f（P）和f′（P）为给定函数（只是水平坐标x，y的函数，因为在S F上z=0）。如果在初始时刻自由面上没有扰动，则f（P）=f′（P）=0；如果运动已经持续很久，像船舶在不规则波中运动的情况，可以认为运动从t=-∞开始，而该时刻的初始条件是零。当然，对这种情况应给出适当的远方辐射条件以取代条件（10.6）。式（10.9）中Z（P，0）为t=0时的自由面形状。在以后任一时刻t，自由面形状为

这时P取在静水面上，即取z=0，场中任一点P的压力：

与前几章类似，上述定解问题也可以采用格林函数法求解。例如，可选择格林函数G（P，Q）具有下列形式，即

式中，P（x，y，z）为场点；Q（ξ，η，ζ）为奇点位置，r（P，Q）、r 1（P，Q）分别是P与Q间的距离和P与Q关于自由面镜像点之间的距离；G*（P，G）是流场中某一调和函数。则对于现在所讨论的不定常问题，在每一瞬时t均成立。即

这里Φ（P，t）应理解为欲求的扰动势，即ΦR或ΦD。其中S为流域的所有边界，它包括物面S 0、自由面S F、底部S B和无穷远处辐射控制面S∞（一般取为半径无限大的垂直圆柱面）；∂／∂v指的是沿边界面S的法线的导数，它当然是施于边界上点Q的。此外，由于∂Φ（P，t）／∂t也是拉普拉斯方程的解，有

式（10.13）和（10.14）中，系数4π是空间立体角，此时P为不在边界面上的某一场点，若P落在光滑边界上，系数则为2π。由于现在所选的G（P，Q）与时间t无关，它不能满足自由面条件（10.3），故若采用上面二式来求解场内速度势，除在物体上须分布奇点（格林函数及其法向偏导外），在自由面上也必须分布奇点。由前几章关于势函数格林函数解法的讨论，自然会产生这样一种想法，即是否可以引进一个新的格林函数，满足一定的边界条件，使得场内的速度势由这一格林函数或其法向导数在物面上的分布即可决定。事实上，考虑到现在边界条件（如自由面条件）的时间相关，类似于第5章频域格林函数问题，可设格林函数为

其中t、τ为时间变量，当τ=t时，上式退化为式（10.12）。注意到G*（P，t；Q，τ）在域内是调和的，故有

于是式（10.14）中的G（P，Q）直接可用G（P，t；Q，τ）取代，即(www.xing528.com)

而且，尽管式（10.17）中出现时间参数τ，但由于式（10.16）的关系，式（10.17）的右端实际上与τ无关。将该式对t由0至τ积分，得到

这里，Φ（P，0）作为初始值，已经引入。注意到Φ的边界条件（10.5）和（10.6）或（10.7），如果要求对有限的τ和t值，G（P，t；Q，τ）满足：

和

则式（10.18）中S B和S∞面上的积分为零，积分边界只剩下物面S 0和自由面S F。鉴于物面条件（10.4）中给出的是而不是，故用关系式：

将式（10.18）中在S 0上的面积分对τ进行分部积分，容易得到

这样，在S 0上的积分中，出现的仅是未知函数Φ（Q，τ）；初始值Φ（Q，0）和是已知的，由物面条件（10.4）给出。为了引进自由面的边界条件，选择G（P，t；Q，τ）在自由面上满足：

那么

这样式（10.21）中右端第一项积分可化为

由于不是给定的，故宜选择G（P，t；Q，τ）满足：

以上式作为格林函数的初始条件，于是式（10.21）化为

注意到Φ（P，0）作为调和函数，有

则有

将上式右端第三行积分进行一次分部积分，则上式可改写成

当场点P落在物面S 0上时，将式中系数4π改作2π，式（10.26）就成为决定物面S 0上势函数Φ（Q，τ）的积分方程。它们对ΦR或ΦD都是适用的。以ΦR为例，在式（10.26）中右端两项中的由物面条件（10.7）给出，即

显然，它们代表物体突然起动后引起的流体运动。在计算时，由式（10.15）可知：

式（10.26）右端含因子，按式（10.9），即为Z（Q，0），代表t=0时刻自由面的初始位移，故该项代表在物体存在的情况下，由自由面初始位移而引起的波浪运动。式（10.26）右端最后一项中，Φ（Q，0）与初始时刻作用于自由表面上的压力冲量Π成比例，即Π=-ρΦ（Q，0），因此，它代表在有物体存在的情况下自由表面上初始压力冲量产生的波浪运动。积分方程的右端项都是已知的，奇点仅须在物面上分布。