船舶波浪运动理论及线性系统响应关系

1）动力学系统

在船舶、海洋平台等工程设计中，需要解决的主要课题之一是确定这些结构在波浪、风等外力作用下的运动、受力、变形等。我们可以把这些结构看作是一个动力学系统（简称系统），波浪等作用叫作系统的输入（激发），结构的运动、受力、变形等称为系统的输出（反应）。系统对输入的作用施行某种变换（见图9.6），结果使函数x（t）变换为另一个函数y（t），即

图9.6　系统对输入的变换

式中，A为算子。

输入x（t）可能有两种情况：一是x（t）本身可能是确定性过程，但受某些随机扰动的影响，因此实际作用于系统的是随机的x（t），须研究如何选用系统的参数使这种扰动的影响为最小；二是输入本身就是随机的，如海浪、风速等，须探讨系统对随机作用的反应。

按运算子的不同，动力系统可分为线性系统和非线性系统两大类。如果运算子具有可叠加性和齐次性，则称为线性系统。这两个性质意味着线性系统对输入的响应等于各个输入分量独立作用时的响应之和。

研究动力系统的最基本的问题是由给定的输入确定系统的反应。稳态线性系统的输出和输入的关系可以写成常系数线性微分方程，如第7章所述的船舶运动方程。对于给定的输入x（t）以及给定的初始条件，该方程式可用经典方法求解，得到y（t）的全解。但对于随机方程，能直接解出上述微分方程的情形是不多的，因为可供利用的数据往往不够充分，且没有简单的试验方法能够确定系数。其次，即使上述微分方程能确定，必须知道x（t）的全部历时过程，才能计算y（t）的全过程，这对随机过程也是很困难的。因此，一般常用频率响应法和脉冲响应法两种方法。

2）频率响应法

因为随机振动可由多数谐和振动叠加而成，故先考虑对谐和振动的反应。设输入是一常幅谐和波，其频率为ω，用复数形式表示成

通过线性系统后的输出也必然具有谐和振动形式，其频率仍为ω，但其振幅和相位会有变化，可用复数因子T（ω）加以考虑。即

复数T（ω）称为频率响应函数或传递函数，它等于输出与输入之比，它的模称为振幅响应算子RAO（response-amplitude operators，RAO），等于输出和输入的振幅比，而其虚部与实部之比等于输出输入间相位差的正切。

根据线性系统的叠加原理，随机输入输出可表示为

频率响应函数T（ω）给出一个系统对于谐和波输入的稳态反应，通过在所有频率上确定T（ω），可完全确定一个系统的动态特性。

3）脉冲响应法

此方法确定系统在适当扰动后的瞬态反应，即自扰动终止的瞬时起，直到系统重新恢复平衡为止的整个过程，测出系统的瞬态反应，从而确定系统的动态特性。

利用单位脉冲函数作为扰动，参见9.2节所述。设在时间t=t k时，单位脉冲函数δ（tt k）作用于系统上（见图9.7），系统反应为h（tt k），称为脉冲响应函数，其典型变化曲线如图9.7所示。

现考虑线性系统对于任意输入x（t）的反应。把x（t）分割成许多脉冲量，在任意时刻t=t k，得

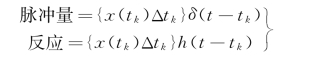
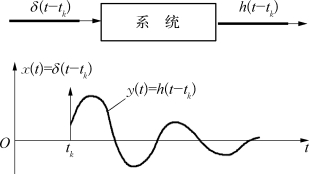
图9.7　脉冲响应函数h（t-t k）

因此，系统的输入和输出为

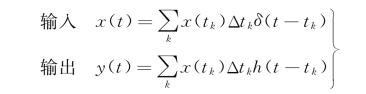
令Δt k→0，输出变成；令t-t k=τ，输出变成τ）h（τ）dτ。

这是x（t）和h（t）的卷积（convolution integral），可写成y（t）=x（t）·h（t），并可在频域写成

此处，H（ω）是脉冲响应函数的傅里叶变换，即

式（9.48）说明，对于线性系统，输出函数的傅里叶变换等于输入函数的傅里叶变换与脉冲响应函数的傅里叶变换的乘积。

4）频率响应函数与脉冲响应函数之间的关系

上述频率响应法是把输入的随机过程，在频域分解成无数频率不同的组成波（余弦波），确定系统对于各组成波的反应，得到频率响应函数T（ω）。脉冲响应法则把输入在时域分割成无数个脉冲，利用单位脉冲函数的概念，确定系统的脉冲响应函数h（t）。T（ω）和h（t）都表征同一系统的动力特性，它们之间必有内在的联系。

如前文所述，线性系统受到频率为ω的谐和激励时，会产生一个同频率的稳态谐和输出。对于输入的随机过程，可把它分解成无数个不同频率的谐和输入。可以认为，它在频带（ω，ω+dω）内的输入分量X（ω）dω将在同一频带内激起相应的输出Y（ω）dω。此时，若该谐和输入为(www.xing528.com)

（理解为它的实部或虚部，下同），则相应的谐和输出为

将以上两式连同式（9.45）和式（9.46）可得

与式（9.48）相比，可得

即频率响应函数（传递函数）T（ω）就是脉冲响应函数h（t）的傅里叶变换H（ω）。

5）输入谱与输出谱之间的关系

由前文所述，可知输入与输出的谱密度函数按定义可写为

将式（9.48）代入可得

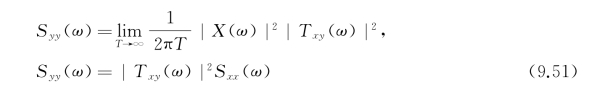
即

这是非常有用的关系式，即只要知道传递函数，就能够由输入谱求得输出谱。

6）传递函数的确定与遭遇频率的影响

确定传递函数T（ω）的方法主要有实验方法和理论分析方法。

实验方法可通过系统在规则激发（余弦波输入）或随机输入作用下通过实验测定。若利用频率响应法在水槽内进行一系列的规则波试验，可以同时得到传递函数T（ω）和相位差，也可以进行脉冲波试验，测得脉冲响应函数h（t）。进行不规则波浪试验时，由输入谱S xx（ω）和输出谱S yy（ω）以及公式（9.51）确定传递函数，此时不能给出相位差，若由输出输入的互谱S xy（ω）和输入谱S xx（ω）求得传递函数时，则可以同时给出相位差。

理论分析时可直接采用频率响应法确定传递函数T（ω），简单起见，参考式（7.51），讨论无航速的海洋平台单自由度的垂荡对入射波的响应，假定平台运动方程如下：

直接令输入ζ（t）=eiωt，且x 3（t）=T（ω）eiωt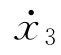，（t）=iωT（ω）eiωt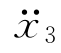，（t）=-ω2T（ω）3eiωt，代入上式并整理可得

显然传递函数T（ω）是复数，包含了幅值响应算子RAO和相位差。

对随机海况下平台运动响应进行谱分析时，可以直接利用公式（9.51）获得运动响应谱，从而进一步预报响应运动的统计特征。

分析船舶海上航行时，假定船舶航行速度为U 0，浪向角为β，船舶在波浪中运动的频率是遭遇频率ωe，参见公式（6.6）。此时系统输入的波浪频率和运动响应频率不一样，需考虑遭遇频率的影响。在改换波谱的频率时，应满足如下条件：

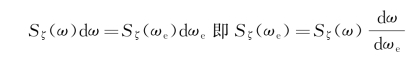
变换可得　

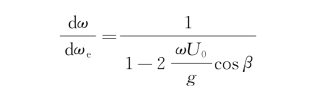
所以有　

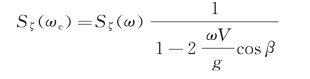
也就是说，进行船舶运动响应谱计算之前，如果响应函数考虑遭遇频率，需要应用上式将波的自然频率谱转到遭遇频率上。即

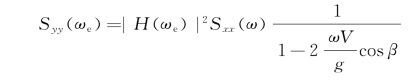
应该指出这一转换有时不一定是必要的。如果可以直接求得以自然波频为自变量的船舶运动响应函数，就仍可直接由式S yy（ω）=|H（ω）|2S xx（ω）计算运动响应谱。