20世纪50年代以来,许多科研工作者对随机海浪做了大量观测与研究。从得到的大量数据中,分析了海浪的各种统计值和谱密度,然后选取某一种表达式作为海浪谱密度的近似表达式。
1)皮尔逊-莫斯科维奇谱(P-M谱)
皮尔逊-莫斯科维奇谱简称P-M谱,它是在20世纪60年代初发展起来的,并在这之后得到广泛应用的一种海浪谱。Moscowitz在1964年对北大西洋1995—1960年的海洋观察资料进行了460次谱分析,得到了随机海浪的平均波谱。之后Pierson和Moscowitz对其进行了无因次化和数学拟合处理,最后得到了P-M谱:
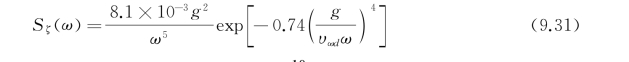
式中,υωd为海面上19.5 m高度处的平均风速,单位为m/s;g为重力加速度,单位为m/s2;Sζ(ω)单位为m2·s。P-M谱有比较充分的观测资料,分析方法也比较有效,所以它能很好地代表真实的充分成长的随机海浪,在海洋工程和船舶工程中得到了广泛应用。图9.4为不同风速下的P-M谱。
在P-M谱中,使用的风速是在海面上19.5 m高度的平均风速。海面上不同高度处的平均风速是不同的,在海面上200 m高度处的风速才接近最大风速。如果已知在海面上某高度z 0处的平均风速,则可以利用Davenport提出的公式:
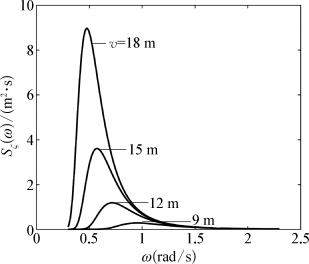
图9.4 不同风速下的P M谱
![]()
来求解z高度处的平均风速,指数0.21是对应于开阔海面的。有义波高与海面上19.5 m高度处的风速的关系可用下式表示:
![]()
如果P-M谱中υωd用h 1/3表示,则式(9.31)变为
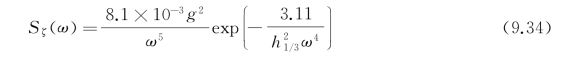
式(9.34)是1966年第11届国际拖曳水池会议(International Towing Tank Conference,ITTC)推荐的波谱,一般称为ITTC单参数波谱。
2)ITTC双参数波谱(ISSC谱)
P--M谱或ITTC单参数波谱是在海浪充分成长情况下给出的,对于非充分成长的海浪,此种波谱有较大误差。在1969年12届ITTC上又提出了采用有义波高h 1/3和特征周期T 1作为波谱的两个参数的ITTC双参波谱
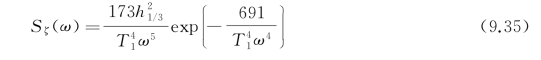
式中,特征周期T 1的单位为s,有义波高h 1/3的单位为m,Sζ(ω)单位为m2·s。T 1和h 1/3也可写成

式中,m 0和m 1是波谱对原点的0阶矩和1阶矩。因为T 1近似于海浪的平均周期T 0,所以式(9.35)也可用T 0代替T 1。
ITTC双参数波谱是第三届国际船舶结构会议(International Ship Structure Conference,ISSC)所采用的波谱,所以也称ISSC谱。1978年第15届ITTC主张不用ITTC单参数波谱,而采用ITTC双参数谱波谱作为ITTC推荐波谱。ITTC双参数波谱适用于非充分成长的海浪。(https://www.xing528.com)
3)JONSWAP谱
英、荷、美、德等国根据“联合北海波浪计划”(Joint North Sea Wave Project,JONSWAP)于1968—1969年在丹麦、德国西海岸以外对海浪进行大量的观察与统计处理,共得到了2 500个波谱,这是迄今为止最系统的一次海浪观测工作,并提出下式作为JONSWAP波谱:
![]()
式中,Sζ(P-- M)表示P -M谱;F为考虑了有限风区影响的修正因子:

式中,γ表示JONSWAP波谱密度的最大值与P-M波谱密度最大值的比值,它表示在有限风区时P--M波谱的峰值升高;ωp为谱峰频率,σp为谱峰形状参数,其值等于:
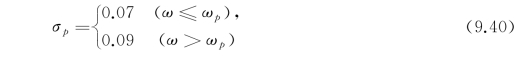
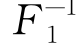 表示在相同风区、风时时JONSWAP波谱曲线下面积与P-M谱曲线下面积之比,1978年第15届ITTC建议采用γ=3.3时的JONSWAP平均波谱作为有限风区波谱,它可以写成
表示在相同风区、风时时JONSWAP波谱曲线下面积与P-M谱曲线下面积之比,1978年第15届ITTC建议采用γ=3.3时的JONSWAP平均波谱作为有限风区波谱,它可以写成
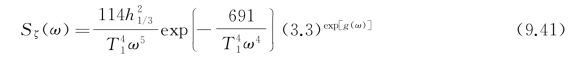
式中,

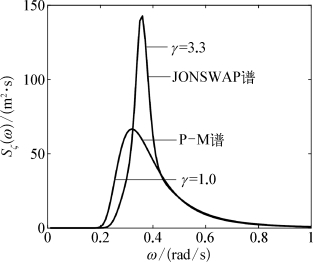
图9.5 JONSWAP波谱曲线形状
图9.5所示为JONSWAP波谱的一般形状,图中也给出了P -M波谱。
4)方向谱
长峰不规则波的海浪谱是假定海浪单一方向传播的,实际海浪除了沿主浪向传播外,还向其他方向扩散,称为短峰不规则波。短峰不规则波可以看成由不同传播方向的长峰不规则波叠加而成。描述海浪沿不同方向组成的波谱,称为方向谱。方向谱的表达式通常引入方向扩展函数D(ω,θ),即
![]()
式中,S(ω)为长峰不规则波的海浪谱;θ为组成波与主浪向的夹角。方向函数D(ω,θ)的一般形式为
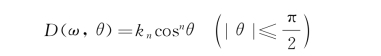
国际船舶结构会议(ISSC)建议采用以下两种n值:![]() ;或
;或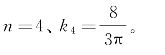
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




