船舶运动理论：随机过程谱分析

1）谱密度函数

随机过程由时域向频域的变换称为随机过程的谱分析。设随机过程X（t）的一个样本为x（t），量值｛x（t）｝2正比于随机过程X（t）的能量，而它相对于时间的平均称为平均能量。一般，它称为随机过程X（t）的均方值。设x（t）代表波面，则平均波能（略去因子ρg）用P x表 示，定义如下：

傅里叶变换可把一个函数由时域x（t）变换到频域X（ω），其变换公式一般写成

此处要把波能由时域的｛x（t）｝2转换成频域，需应用巴什瓦（Parseval）定理，即

上式左边为随机过程在时段（-∞，∞）内的总能量，故右边|X（ω）|2为x（t）的能谱密度的一种形式。

现利用傅里叶变换证明巴什瓦定理：

若令x 1（t）=x 2（t）=x（t），则X 1（ω）=X 2（ω）=X（ω），根据定义和复数公式即可得证巴什瓦定理。

现应用巴什瓦定理把平均波能转换成频域表示：

如下，定义记录x T（t）的谱密度函数：

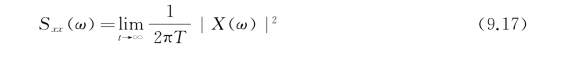
它们是圆频率ω的函数，由此可得

式（9.18）表明，谱密度函数下的面积等于平均波能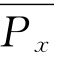（略去ρg），故把S xx（ω）称为能量谱密度，它表示能量相对于频率的分布。为了得到谱密度的具体形式，除了可由傅里叶变换得到X（ω）代入前述公式外，一种常用的方法是通过随机过程的自相关函数和维纳-辛钦定理进行估算。

2）自相关函数与维纳-辛钦定理

对于各态历经随机过程，可由一个现实确定自相关函数：

显而易见，自相关函数的单位是X 2的单位。另外，根据傅里叶变换公式，可得

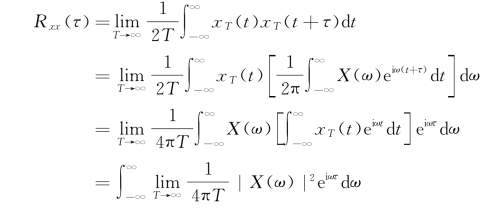
即

此即为维纳-辛钦（Wiener-Khintchine）定理，它可表述为：若随机过程是弱平稳的，则其自相关函数和谱密度函数之间存在傅里叶变换的关系。但公式中积分前的系数有时不同，工程上则常用单侧谱，故上式可改写为

通常由傅里叶变换得到的是复函数，因此S xx（ω）可用实部和虚部两部分表示。当随机过程是实函数时，S xx（ω）和R xx（τ）都是偶函数，而sinτ是奇函数，乘积R xx（τ）sinτ也是奇函数。根据积分区间的对称性和奇偶函数性质，可以得到下列常用的关系式：

3）窄带谱和宽带谱随机过程(www.xing528.com)

一个随机过程，若其谱密度分布在很窄的频率范围内，如图9.1（a）所示，则称之为窄带谱随机过程，它的自相关函数如图9.1（b）所示。理想化的规则波可视为窄带谱随机过程的极限情况，其能量集中在某一频率上，频带宽度为无限小，其谱密度函数可用脉冲函数表示。

单位脉冲函数（unit impulse function）也称狄拉克δ函数（Dirac delta function），δ（t-t k）的定义为

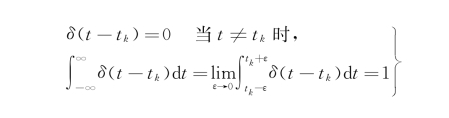
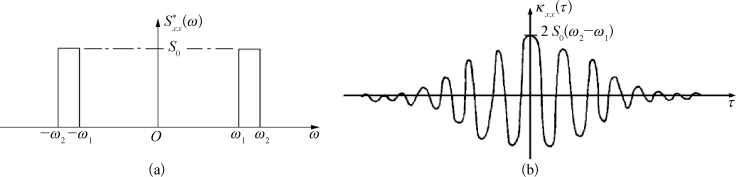
图9.1　窄带谱随机过程的谱密度和自相关函数

（a）谱密度分布；（b）自相关函数

δ（t-t k）函数代表集中于一瞬间或某一点（t=t k）处的单位量，如图9.2所示。设规则波的频率为ω0，能量为规则波的谱可表示为

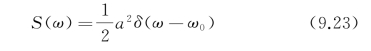
宽带谱随机过程的谱密度存在于较宽的频带内，其时间过程是由整个频带中各种频率信号叠加而成的，波形极不规则，波峰波谷上常有小波。　

4）谱矩和谱宽参数

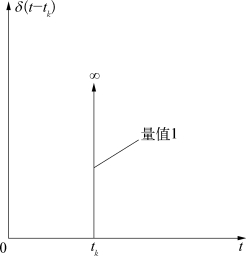
图9.2　单位脉冲函数

海浪谱一般有如图9.3所示的形状，但其宽窄程度各不相同。海浪谱不仅给出了海浪能量分布的内部结构，根据海浪谱还可以计算出一些外观统计特征，故海浪谱有着重要的理论意义和广泛的应用价值。为使功率谱应用方便，人们定义了一些旨在反映谱在某方面的特征的量，而其中最为常见的是谱矩和谱宽的概念。

谱矩的定义式为

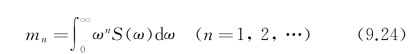
显然，谱的零阶矩m 0等于波面位移的方差，

即m 0为单位波面内波动平均总能量（功率）的量度。由式（9.24）可推导，阶数越高（即n越大）的谱矩越凸显高频部分的特性。一般说，一阶和二阶谱矩m 1和m 2主要反映谱含能段的特性，而高阶谱矩则主要反映高频部分的特性。谱密度的二阶矩等于速度的方差，谱密度的四阶矩等于加速度的方差。

根据上述矩的计算可以得到海浪的特征波高和特征周期：

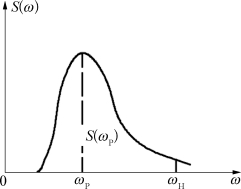
图9.3　海浪谱

谱宽度是波谱宽窄的量度，它反映了谱内能量的集中程度：谱宽度大反映了海浪能量相对于频率的分布分散，谱宽度小则反映能量集中于某频谱附近。谱宽参数ε是Cartwright推导正态过程波面极大值分布函数中建议采用的无因次量：

式中，Δ可以表示为

由此可见，Δ≥0，从而ε≥0。由式（9.28）可知，由于m 22／m 0m 4≥0，故有

此外，由式（9.29）可知，若谱S（ω）的能量集中于频率谱，则ω1与ω2很接近，于是（ω21-ω22）2很小，当S（ω）全集中于一个频率时，则ω1=ω2，于是ε=0；如谱的能量分布很分散，则ω1与ω2相差很大，于是ε→1。由此可见，ε可反映谱内能量集中的程度，理论上其值可无限接近0或1。