船舶波浪力计算方法及应用

前文讨论辐射势而引入切片方法时，根据船体细长假定，且在物体附近，流动主要受船体形状制约，使流动参数沿纵向的变化缓慢，从而将三维拉普拉斯方程演化为二维拉普拉斯方程，且自由面条件和物面条件也相应变化。这样，纵向变量x仅作为一个参数出现，辐射势和辐射力的求解可在各指定的横截面内按二维流动进行，船体所受总的辐射力可按各横截面受力叠加而求得，参见式（8.9）。当计算波浪力时，绕射势是由入射波遇到船体而产生的，船体细长，绕射势沿船体纵向的变化是否仍然缓慢是需要进一步考察的。

先看入射波速度势ΦI，它由式（6.17）给出，略去取实部的符号，ΦI可写成

式中，A为入射波波幅；ω0为波浪自然频率；ω为遭遇频率；β为浪向角；k为波数；H为水深，当H→∞时，。上式在x方向的偏导数是

ΦI在其他方向的偏导数：

相比，仅在cosβ≪1的横浪情况下才可以认为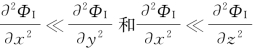，三维拉斯方程才能退化成二维拉普拉斯方程。在一般情况下，特别是迎浪状态，入射波参数沿x方向的变化显然不是缓变的；作为绕射波，它一方面取决于入射波，另一方面在船体附近又受船体形状的约束。我们不妨假定绕射势ΦD的形式是

式中，φd（x，y，z）沿x方向的变化是缓慢的。将上式代入控制流动的三维拉普拉斯方程，并略去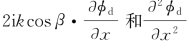等缓变项，得到相应的控制方程为

这是一个二维的亥姆霍兹（Helmholtz）方程。

将式（8.15）代入自由面方程式（6.19），略去含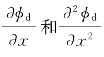的项后，得到φd要满足的自由面条件为

式中，ω0=ω+k U 0cosβ是波浪的自然频率。

将式（8.14）和（8.15）代入物面条件式（6.20），略去含单位法线矢量纵向分量x 1的项，得到

式中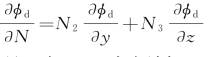，是在横剖面周线上的法线导数，N则为横剖面周线上的法线单位矢量。式（8.18）中右端仅N 2，N 3中含参数x，按船体细长的假定，它们随x的变化应该是缓慢的，这反过来正好表明φd随x是缓变的。

式（8.16）、（8.17）和（8.18）就是二维绕射势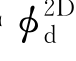应满足的方程和条件，当然，还应补充池底条件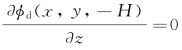和适当的辐射条件。值得指出的是，在船舶有航速时，ΦD的振荡频率是遭遇频率ω，但φd的自由面条件中含有的频率参数却是波浪的自然频率ω0，这一点可从式（8.15）和（8.17）中看出。

与辐射问题的情况一样，要使式（8.17）中保留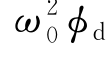项，要求波浪频率较高，即ω0=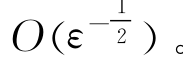。这时各横剖面上的流动互不干扰，φd（x，y，z）中不含任意函数f（x），即三维的φd等于二维的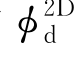，即

针对亥姆霍兹方程，同样可以找出格林函数和应用格林函数法求解。有兴趣的读者可自行推导。

将得到的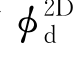和式（8.15）代入式（6.28），可得切片理论中的绕射力为(www.xing528.com)

式中，C（x）是纵坐标为x处的横剖面的平均湿周线，d l是沿C（x）的弧段。

应用哈斯金特关系，可以不用求解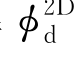而直接从二维辐射势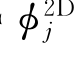得到波浪力的表达。

在上节中已经谈到，在船体细长的假定下，φj可用相应的二维辐射势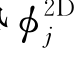表示。在无航速时，由式（6.32）可得

有航速时，φj应用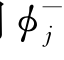代替。在细长体假定下，φj和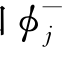的自由面条件变成一样了，即

相应地，二维辐射势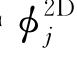也完全相同。代入式（6.35），得波浪力：

上述F Wj=Re｛f Wje-iωt｝。

有时，在工程应用中还采用下列办法以谋求更进一步的简化。在物面横剖面周线C（x）上，可表示成

在绕射力中与同时出现的是下述类型的积分：

如果船体横向尺度相当小，上述积分中的因子tanh k（z+H）·ΦI和ΦI可用剖面上某一点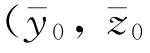）上的数值来代替而视作常数，于是

其中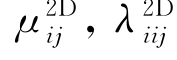是二维剖面的附加质量和阻尼系数，其定义（见8.1节）是对左右对称的船体横剖面，可取作零。

无论是式（8.22）或式（8.24），只要辐射势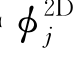已知，即可求出波浪力，而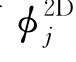在辐射力或附加质量和阻尼系数的计算中是必不可少的。

对方艉船型，同样可引进艉端修正。波浪力的艉端修正项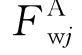为［9］：

该修正项可补充到式（8.22）中。

至此，按切片方法已建立了船舶流体动力系数（附加质量和阻尼系数）及波浪力的表达式，将其代入运动方程式（7.35）或式（7.36）即可用于船舶在波浪上的运动计算。当然，按切片理论，只能计算除纵荡外的五个自由度的运动。纵荡运动的计算，常按一些物理直观上的考虑单独建立运动方程来进行，读者可参考文献［162］。