参考坐标系下的船体运动方程

上述运动方程的建立，是以船舶质心（重心）与动坐标系原点重合的假定为前提的。但是，当我们讨论辐射问题或绕射问题以决定流体作用力时，已选定参考坐标系的坐标原点位于静止时的自由表面上。若船舶无摇荡运动，动坐标系与参考坐标系重合。显然，在一般情况下船舶重心不会恰好与坐标原点重合，这就需要对运动方程进行修正。办法不外乎两种，或者改变运动方程使之与求解流体动力时所用的坐标系一致，或者把所求得的流体动力变换到以重心为原点的坐标系中。本节将讨论前者。

如图7.2所示，设有一动坐标系与刚体固结在一起，原点在o点，这一动坐标系记以oxyz。质心c在此坐标系中的位置矢量是r c。在c点上也固结一动坐标系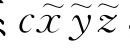，它的三个坐标轴始终与坐标系oxyz的相应的坐标轴平行。

图7.2　坐标系的转换

以上所建立的运动方程是相对于动坐标系的，现在的任务是要把运动方程变换到动坐标系oxyz中去。

已经知道，以质心c为基础的运动方程是

这里

式中，M为刚体质量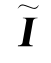；是定义在坐标系中的质量惯性矩张量，它定义为

式中，v c是质心运动速度；ω为绕质心的转动角速度，F为外力矢量；M c为相对质心的外力矩矢量。

考虑到由惯性坐标系向动坐标系转换时有如下关系：

且在动坐标系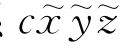中与时间无关，故方程（7.39）又可改写成

该式即为动坐标系中的刚体运动方程。

由于

式中，v 0是o点移动的速度矢量，ω是刚体转动的瞬时角速度，式（7.42）中的第一式进而可写成

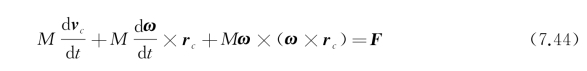
这里利用了关系式，这是因为r c的数值虽然不变，但由于刚体在转动，矢量r c也是转动的。

将式（7.44）展开，其表达式为

在一阶近似的理论中，上式左端的第二个矩阵中各元素均含有二阶小量ωiωj（i，j=1，2，3），故实际上可以略去。

式（7.42）中第二式为绕质心的动量矩定理，我们也可将其变换成绕o点的动量矩定理形式。

由于

可得

其中应用F的表达式（7.44）。将上式展开并略加整理，可得如下的表达式：

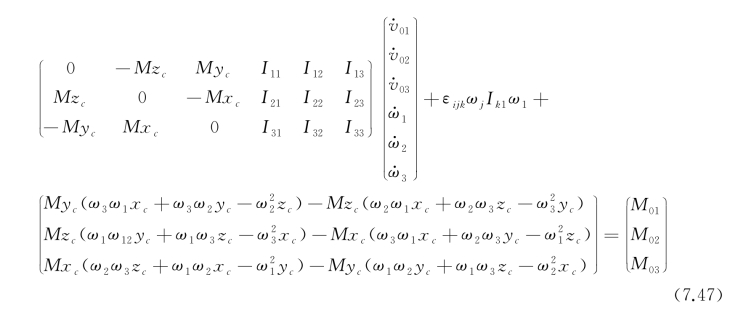
式中，其余Mx cix cj（i，j=1，2，3；i≠j）。同样，在一阶近似中，上式左端第二和第三个矩阵可以略去。

如把式（7.45）和式（7.47）合并，并略去二阶量，则可得在坐标系oxyz中表达的一阶运动方程：

(www.xing528.com)

这里U是广义的速度矢量，定义为

F是广义力矢量，定义为

［M］是一个矩阵，其定义为

［M］称为惯性矩阵。

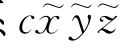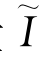当船体有初始倾斜时，相当于固结于c的动坐标系一开始与坐标系就不重合，如图7.3所示，记作c。按习惯，船舶转动惯量仍在坐标系中表示，而运动方程中用的转动惯量则是在坐标系的数值，这中间亦应有个转换关系。

上述两个坐标系的变量关系：

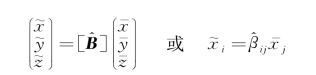
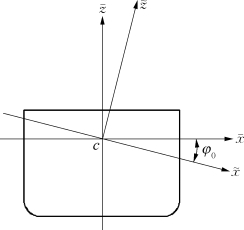
图7.3　有初始倾斜的情况

其中=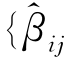j｝为转换矩阵。

于是可表示成

若设船舶有一初始横倾角φ0，则

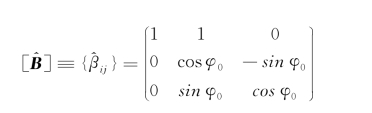
又若船舶关于坐标系是左右、前后对称的，则在此坐标系中的惯性矩张量为

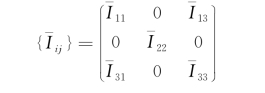
按式（7.50）得

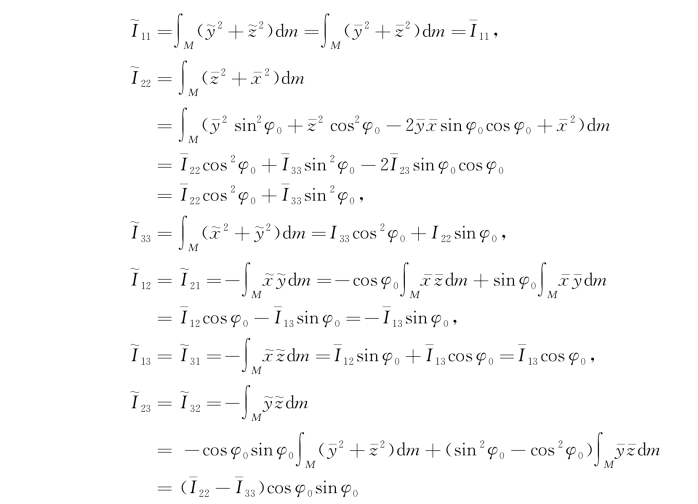
归纳以上各式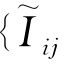，｛｝可写成

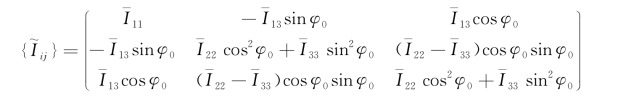
应用上式即可计算运动方程中惯性矩阵的I ij（i，j=1，2，3）。

在运动方程（7.48）中，广义力F i中所含的静恢复力部分亦应按船重心所在位置进行修正。船体对称、正浮时，主要是横摇恢复力矩和纵摇恢复力矩需要修正，修正的方法可按式（7.32）及其紧接的说明进行。

类似于式（7.35），在参考坐标系下，船体的线性频域运动方程最终可表达为

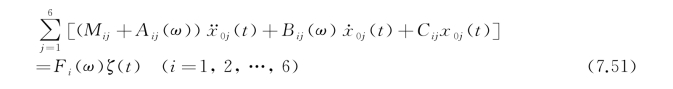
如果设船舶的运动x（t）与干扰波浪同为频率ω的正弦振荡。则按照正弦运动的求导法则

将这些关系式代入上面的耦合运动方程中，得到六个运动自由度的频域微分方程如下：

式中，

式（7.53）表示方程中矩阵的元素K ij（ω）是由与船舶有关的质量M ij、附加质量A kj（ω）以及阻尼系数B ij（ω）等有关参数组成的，它们均为频率的函数。而波浪干扰力系数F i（ω）则表示单位振幅的频率为ω的规则波，在第i个运动模态内的干扰力（力矩）的幅值。注意所有的量均为复数，代表一频率为ω的振荡量的复数振幅。