船舶波浪运动理论：流体静恢复力简介

本节讨论式（7.18）和（7.19）中的静力项。注意到法向矢量是指向物体内部的，可以证明下列各式成立，即

式中，A W为静止时水线面积，Δ是排水体积，是水线面漂心纵坐标；是水线面漂心的横坐标，如果船体关于纵舯剖面对称，则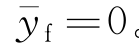。于是式（7.18）中静力项为

式中，横方向的静力项分别与船体重力在动坐标系横轴上的分量平衡，垂向力中第一项为船体的静浮力，它与船体重量平衡，这些力实际上无须进入运动方程。垂向力中第二项是由于船体垂荡引起的浮力变化，在线性范围内，它与垂荡位移成正比，而方向相反，形成垂向的静恢复力（restoring force）；第三项和第四项则为船体横、纵摇时引起的垂向静力项。由此可见，在三个线位移振荡运动中，只有垂荡运动有恢复力存在，纵荡和横荡运动不存在流体静恢复力。

类似地，关于o点的静力矩在动坐标轴上的投影是

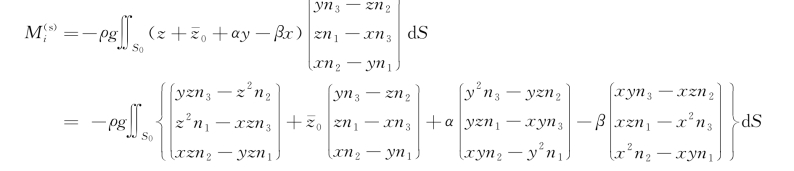
不难证明

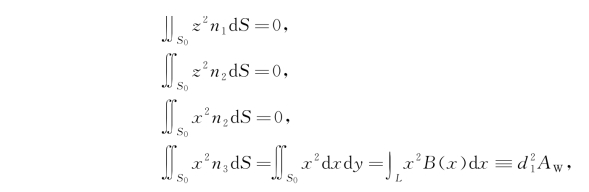
式中，B（x）为水线宽度；l（z）为在某一z处水线长度；A W是水线面积；d 1和d 2分别是水线面绕oy和ox轴的惯性半径；Δ为排水体积，x B，y B，z B为船体正浮时的浮心坐标。于是可写成

(www.xing528.com)

式中，ρgy BΔ和-ρgx B是船体正浮时，浮力不通过o点时造成的横倾和纵倾力矩，它们和重力构成力偶，决定船体振荡的平均位置。其余各项是由于船体偏离平衡位置而造成的对o点的力矩。绕垂直轴转动力矩的出现，是由于它是在动坐标轴上的分量，事实上它与重力的转动形成的力矩互相平衡。因此，实际上要纳入运动方程的静水力矩是

其中与的意义自明。现在对和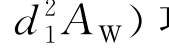项加以说明，因两者相似，一是横倾，一是纵倾，故仅以前者为例，后者可类推。

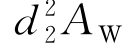力矩与α的方向相反，是回复性的。是水线面对纵轴ox的横向惯性矩，即

根据船舶静力学，横摇至某一角度时，正浮状态时的浮心C移到C 1（见图7.1），距离CC 1为［157］

故

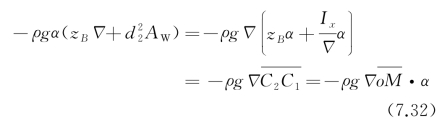
式中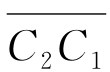，及的意义如图7.1所示。注意到现在设定船舶重心与坐标原点o重合，故由图可知，这一项其实就是浮力对ox轴的力矩，它与重力形成一个力偶。这个力偶的矩促使船体回复到其平衡位置，故称恢复力矩或回复力矩。一般地，当重心G与坐标原点o不重合（但仍在o M连线上，即坐标轴oz上），式（7.32）中的o M应修正为GM，该量在船舶静力学中定义为横向初稳心高度。对纵倾力矩有完全类似的表达。

图7.1　横摇恢复力矩