船舶运动理论：流体动力及阻力分析

由于物体运动是个小量，瞬时湿表面与静止时的湿表面或平均湿表面S 0相差为ε量级。不妨令S=S 0+ΔS，而ΔS=O（ε）。因此，准确到ε一阶量时，上式中的S可简单地用S 0代替。

式（7.18）和（7.19）中

它们是波浪作用下船体运动产生的动力项，可应用之前定义过的广义力矢量F i和广义法线矢量n（i=1，2，3，4，5，6）记作

余下的则是静力项，以后用上标（S）记之。

对一阶近似，场内速度势要满足的拉普拉斯方程和边界条件都是线性的，可应用叠加原理把速度势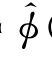（x，y，z，t）加以分解（参见4.5节），即令

严格来说，上述速度势中变量应在参考坐标系中表达。但既然船体的摇荡运动是小量，且一阶势的物面条件已经变换成在物面的平均位置上满足，就没有必要在此严格地区分动坐标系变量（x，y，z）和参考系变量（x′，y′，z′），由此而来的误差将是比φ⁀更高阶的小量［参见4.5节及式（7.17）的展开］。

设入射波是单向的规则波，其速度势为

式中各个量的意义已在第6章定义过，不再重复。按约定，我们实际上应取上式的实部才是物理上的速度势。上式表明，在船上看来，入射波是一个以频率为遭遇频率ω行进的波，在它的长时间的作用下，瞬态现象（transient phenomena）消失，船体也将以该频率作稳态简谐振荡，即运动位移：

式中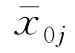，为振荡运动的复数幅值。场内辐射势ΦR和绕射势ΦD中也将含振荡因子e-iωt。关于它们已在前两章分别作过详细阐述。

一般地，辐射势ΦR还可分解成

式中，j=1，2，3，4，5，6指运动的模态；φj为相应于j运动模态的规范化速度势。于是场内总速度势可记为

将其代入式（7.20）可将流体动力分成以下三个部分：(www.xing528.com)

第一部分是，它给出物体定常移动兴波所产生的定常阻力。在处理摇荡问题时，这部分力是不计的，或者说它已由船舶的推进力平衡。

第二部分力总称波浪扰动力，为

其中

前者为熟知的傅汝德-克雷洛夫力，后者为波浪绕射力。它们还可进一步化成式（6.27）、（6.28）或（6.35）作具体计算。

第三部分力与φj相联系，系船体运动遭受的流体反作用力，称辐射力。应用

可把含φj的几项写成

其中

上述各项已在第5章中作了讨论。事实上，A ij中包括了流体附加质量和阻尼系数，若令

则式（7.27）的辐射力又可记为

式中第一部分为附加质量力，后一部分为阻尼力（如前所述，μij定义为附加质量，λij定义为阻尼系数）。