船舶波浪力计算原理及公式

一旦场内的绕射势ΦD求得，则散射势Φ即为ΦD与入射波速度势ΦI之和。限于一阶近似，流场中的动压力为

作用在物体上的波浪力：

或者

式中，φ=φI+φD；S 0为物体静置于静水中时的湿面积；下标j=1，2，3，…，6，指力的方向和广义法向矢量的投影方向。

将φ=φI+φD代入式（6.24），则波浪力可分解成两部分，即

其中

这里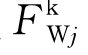（或）称作傅汝德-克雷洛夫力，它可视为不计物体存在对入射波流场的影响的情况下得到的波浪力。由式（6.17）可得

于是

其中ω+U 0k cosβ=ω0正好是波浪的自然频率。对给定的φI，如式（6.28），这部分波浪力是很容易计算的。

或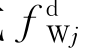叫绕射力（diffraction force）。如采用格林函数法求解φD，则式（6.26）也不难计算。事实上，若略去作为高阶小量的沿水线的积分项，我们还可以应用推广的斯托克斯公式将消除，最终得到

哈斯金特［155］关于无航速的情形推导了一个重要关系式，利用它可以不必求解绕射势，直接由波浪速度势φI和辐射势φj（j指运动模态）求得波浪力。而辐射势在求船体附加质量和阻尼系数时就已经解决了。

可以证明

式中，φj是相应于j模态运动的单位速度辐射势，由φj的边界条件而引入上式。由于φD在物面上的边界条件是，故按式（6.29）有

式（6.28）中各项均可按上式变换之。这样，对给定的入射波速度势φI，一旦解出辐射势φj，不必求得绕射势即可算出绕射力。

事实上，若取由物面S 0、自由面F、池底B和半径R为无限大的圆柱面Σ所围的流体域τ，在τ内绕射势φD和任一辐射势φj都是调和的。由格林公式得

由于池底条件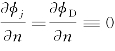，故沿池底B的积分为零。辐射条件：

保证了沿圆柱面Σ上的积分亦为零。再按无航速时的自由面条件：

注意φj和φD均满足上式，则(www.xing528.com)

于是式（6.31）变成

即关系式（6.29）得证。

将傅汝德　克-雷洛夫力和绕射力合并在一起，无航速情况下，物体遭受的波浪力为

这就是著名的哈斯金特关系或哈斯金特公式。注意到

和

则式（6.32a）又可写成

若在流域τ中再次应用格林公式，注意到φI满足同样的池底条件和自由面条件，但不满足辐射条件，可将式（6.32a）改写成

这也是哈斯金特关系的一种形式，只要知道φj在无穷远处的渐近形式，就可以根据其计算波浪力。

有航速时，自由面条件：

这时式（6.31）中沿自由面上的积分无法消除。纽曼［156］引入反向移动的辐射势，以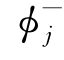表示之，它满足的自由面条件：

式（6.31）中以代替φj，则沿自由面的积分变为

其中积分曲线C为物体与静水面的交线，即水线。对细长体来说，d y=d l sinθ，d l为曲线C上所截的微段，θ为d l与ox轴的夹角，是个小量，因此上述沿周线C的线积分将是高阶小量，可以略去。即认为上述沿自由面的积分近似为零。在计及辐射条件而沿圆柱面Σ的积分为零的情况下，最终得到

注意到反向移动辐射势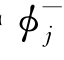在物面上满足条件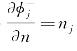，式（6.28）中的绕射势φD可按上式消除之，于是波浪力可表达为

这里有一点应该强调，即对于来说，U 0的方向虽然改变了，但频率ω仍然是以正U 0方向移动时与波浪的遭遇频率。

若引入

这里表示不显含速度U 0的那部分波浪力，表示显含速度U 0的波浪力部分，则式（6.35a）可记作