船舶波浪上的绕射问题

绕射问题中不考虑物体的摇荡运动，只计入波浪与固定的或以定常速度移动的物体之间的流体动力干扰。

如果物体有定常移动速度U 0而无振荡，则物体将产生移动兴波。相对于以速度U 0移动的参考坐标系来说，由定常移动产生的兴波是定常的；定常速度势记为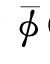（x，y，z）。整个流场中的总速度势在参考系中记为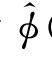（x，y，z，t），它可以表示成（参见4.5节）：

式中，ФI为入射波速度势，ФD为绕射速度势；这两者之和构成了场内总的不定常速度势部分Φ（x，y，z，t）。Ф也常被称作散射势（scattering potential）。

如4.5节中所指出，如果对物体形状加以限制，要求它的定常兴波势φ-是小量（ε一阶量级），则在一阶线性近似中，定常势φ-与散射势Ф的定解问题可截然分开，即认为两者间互不影响。这时，散射势Ф满足的自由面条件为

自由面形状为

这一条件在形式上与有航速时的辐射势没有什么区别。由于入射波势ФI满足式（6.13），故绕射势ФD要满足的自由面条件亦是式（6.13）。而且，在自由面形状上，波面坐标ζI和ζD亦可以线性叠加，它们分别由式（6.14）用相应的速度势确定之。

在绕射问题中，物面条件比较简单。相对于移动参考坐标系来考察，物面S 0是不随时间改变的，故一般有

在S 0上满足。又因定常移动兴波势φ-满足的物面条件为

故恒有

此外，绕射势ФD还应该满足池底条件和辐射条件。

由第3章讨论中已知，入射波的速度势ΦI是已知的，准确到一阶，ΦI表达式为(www.xing528.com)

它是由式（3.50）得来的。即先将该式变换到空间固定坐标系中，再变换到与船体一起移动的参考坐标系中，并考虑到入射波与船体运动间的方向差异，具体做法与式（6.4）的推导过程类似。这时，在参考系中的表观波浪频率已不是其自然频率ω0=kC 0，而是遭遇频率ω=ω0-k U 0cosβ。

式（6.16）还可改写成

式中，为速度势ФI中独立于时间的部分；符号Re表示取后续物理量的实部。

相应地，设绕射势ФD表达式为

为叙述方便起见，常略去符号Re，而约定取不定常势复数表达的实数部分。

按式（6.13）和（6.15）容易求得绕射势定常部分φD须满足的自由面条件和物面条件分别如下：

此外，φD显然必须满足拉普拉斯方程及池底条件：

以及适当的辐射条件。考虑其物理意义，第5章中述及的移动脉动源速度势的辐射条件套用过来是恰当的，尽管目前场内绕射势的脉动不是由物体振荡引起，而是由入射波速度势的脉动所产生。

比较φD的定解问题与第5章中有航速船舶辐射势的定解问题式（5.64），不难看出两者间唯一的不同表现在物面条件［S］上，但这种差异并不是实质性的。因此，绕射势φD可与辐射势同样地求解，比如利用格林函数法，只需在积分方程中将右端项改作即可。

在航速U 0等于零的特殊情况中，绕射势φD的定解问题即与5.2节所述的无航速船舶辐射势的定解问题类似，差别在于物面条件。不难类推，这时φD仍可利用格林函数法求得，当然这时物面上分布的将不是移动脉动源而是纯脉动源（详见5.5.2节），其计算相对来说简单一些。