船舶运动理论：遭遇频率与自然频率

第3章中已经证明，准确到三阶小量，无限深水中入射波的速度势可以用其线性项的表达式（3.69）来表示，它在固定坐标系中的形式：

式中，波速C由式（3.64）确定，波浪圆频率ω0定义为

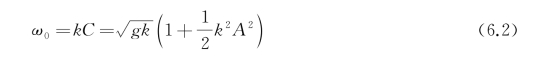
式中，k为波数，A为来波波幅。式（6.1）是在假定波浪沿ox轴正向传播时得到的。然而，在船舶运动的问题中，ox轴常取为船舶的前进速度方向，故波浪的传播方向不一定与之重合。一般地，可认为波浪传播方向与ox轴正向成一夹角β。则波浪速度势可由式（6.1）经坐标旋转后得到，即

β角称为波向角或浪向角（wave angle），上式即为浪向角为β时的入射波速度势。在习惯上，把β＜30°范围内的波浪称为随浪（following sea），当β=0°时波向与船的航向一致；β于60°～120°之间的波浪统称横浪（beam sea），β=90°时，波从船侧传来，也称为正横浪；当浪向角β在150°～180°之间时，称为迎浪（head sea），β=180°则表征波从船的正前方传来；浪向角在30°＜β＜60°和120°＜β＜150°范围内，则波浪分别称为艉斜浪（quartering sea）和艏斜浪（bow sea）（见图6.1）。

波浪速度势的上述表达式都是在空间固定坐标系中表达的。如果船以航速U 0沿ox轴正向前进，对于与船一起以速度U 0移动的参考坐标系来说，x=x′+U 0t，y=y′，z=z′，代入式（6.3）并整理，前进波的速度势变成

图6.1　波浪方向的定义

上式中定义

习惯上称ω为遭遇频率（encounter frequency），相应地，波浪本身的频率ω0称作波浪的自然频率（natural frequency）。式（6.5）表征了航速对表观频率的影响，也就是说船上的观察者所感觉到的波浪频率不再是波浪的自然频率，而是遭遇频率。这一影响称为多普勒（Doppler）效应。

当波浪从船的侧前方入射时，β＞90°，cosβ＜0，式（6.5）中U 0的出现，总是使遭遇频率增加。容易证明，这时波浪自然频率与遭遇频率之间是一一对应的。如果波浪从船的侧后方赶来，则β＜90°，cosβ＞0，情况就变得复杂起来。由式（6.5）知，U 0的出现将减小遭遇频率，在ω0＞kU 0cosβ时，遭遇频率ω＞0，表观上波浪仍然从船后赶来，只是波浪周期和波长显得长了。当ω0=k U 0cosβ时，遭遇频率为零，波和船一起前进，两者呈相对静止状态。对于给定的浪向角β，有一个确定的ω0（≠0）满足这相对静止的关系。当ω0＜k U 0cosβ时，遭遇频率竟然是负的。从物理上考虑，振荡频率当然不会是负的，只是本来从船侧后方传来的波对船上的观察者来说，现在已变成从侧前方传来。采取这种解释，从而允许遭遇频率可以是负的。

由于k是ω0的函数［参见式（6.2）］，对给定的自然频率ω0和航速U 0、浪向角β（一般还应有波幅），可按式（6.5）计算出唯一的遭遇频率ω0。但是，对给定的遭遇频率，在β＜90°时，情况就不同了。对实际给出的遭遇频率的数值，首先要设定它是正的或是负的。为了确定起见，下面的讨论中，略去色散关系（6.2）中的项，即限于二阶波浪理论。这时k=／g，而多普勒效应为

先设定ω＜0。令|ω|=M，ω=-M，代入式（6.6），得到

可解得对应的自然频率(www.xing528.com)

其中一个负根是无意义的，应予舍弃。它表明，在ω＜0时，遭遇频率与波浪自然频率之间是一一对应的。

再设定ω＞0，令ω=M，代入式（6.6），得到

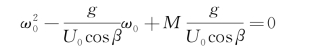
由此可解出对应的波浪自然频率

将它绘成图6.2。

图6.2　极坐标系（U 0ω0／g，β）中遭遇频率与波浪自然频率间的关系

当M=0，也就是遭遇频率是零的时候，对应的波浪自然频率是ω0=0和ω0=g／U 0cosβ。在极坐标系（U 0ω0／g，β）中，前者为坐标系原点，后者即（U 0ω0／g）cosβ=1，相当于U 0ω0／g在β=0的横轴上的投影恒为1.0，它代表一条垂直线，在横轴上的截距1。该直线的右边的曲线，对应于ω＜0，其解由式（6.7）给出，对给定的ω=-M（M＞0）有一个点（U 0ω0／g，β）与之对应。在直线ω=0的左边，是ω＞0的情形，其解由式（6.8）给出。式（6.8）中的根号为零时，对应的有

它是与横轴截距为的一根垂直线，对应的M值是

当β=0时，M=M 0。随着β的增加，沿着直线［式（6.9）］有M＞M 0。

对的情形和β的曲线是

其形状颇似一条以为渐近线的“叶形曲线”。对于一个波向角β，有两个值与之对应。一般在M≠M 0时，式（6.11）可写成

若M＜M 0，对应于“+”号和“-”号，分别有两条曲线，一条在叶形曲线封闭环的内部，一条夹在叶形曲线右支与渐近线与之对应。若M＞M 0，存在一个极小的βmin=cos-1（M 0／M），当β＞βmin时，根号内的数值是负的，无实根；当β＞βmin时，对同一波向角，也有两个之间。对于一个波向角，也有两个与之对应。

以上即在航速影响下，遭遇频率与波浪自然频率的关系，它在应用谱分析技术寻求船舶在不规则波浪上的统计运动特性时有一定的重要性。因为波浪谱是以自然频率为基础的，而船舶在规则波上的响应则是以遭遇频率为基础的，将两者沟通时，需要依据上述关系将频率加以转换。有兴趣的读者还可参考圣·丹尼斯和皮尔逊的论文［154］。上述论点对有限水深和有限振幅的斯托克斯波也适用，唯具体关系会有些不同。