船舶波浪运动理论：常数面元法计算结果与图示

波浪中的浮标振荡辐射问题，可以采用无航速的格林函数法求解其辐射力。图5.13、图5.14为常数面元法计算所得的浮标辐射水动力系数。浮标半径为5 m，水线面中心与浮标重心及几何中心重合，浮标平均湿表面分布了318个面元（见图5.12）。纵荡和垂荡的水动力系数的计算结果采用了无量纲化的形式表达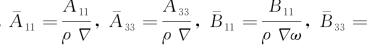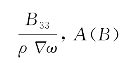为频域附加质量（阻尼系数），ρ为水的密度，Δ为浮体的排水体积，ω为入射波频率，k为波数，a为波幅。

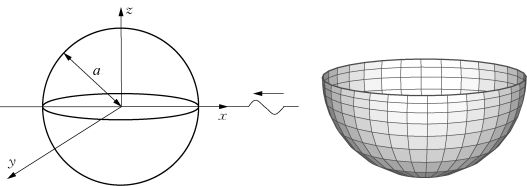
图5.12　浮标坐标系与平均湿表面的离散网格

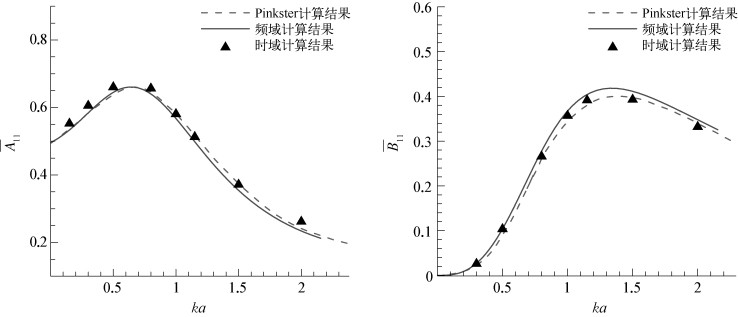
图5.13　纵荡附加质量和阻尼系数

对于无航速的频域格林函数的计算较为完美，如Newman［149］等对积分核在不同积分区域展开成级数计算分析，其采用多项式拟合逼近，计算速度快，结果稳定，是商用软件WAMIT的计算核心基础。由于有航速问题的复杂性，真正按移动脉动源直接进行计算的结果不多。以下将简述洪亮在给出的水平线段格林函数法的计算结果［64］，即面元上的格林函数积分，采用面元上几条水平线段上的积分值之和来替代，水平线段上的格林函数积分处理采取空间积分先于双重积分进行。计算时，首先需要在垂直方向上将船体上的每个面元离散为若干水平线段。图5.15给出了WigleyⅢ船体网格划分的示意图，最靠近自由面的面元被离散为4条水平线段而其他面元则被离散为2条水平线段，每条水平线段的位置是根据面元垂向长度按照高斯积分中高斯点的位置来确定的，如图5.16所示。

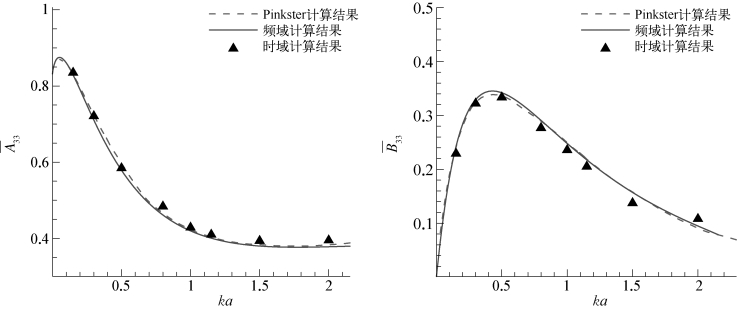
图5.14　垂荡附加质量和阻尼系数

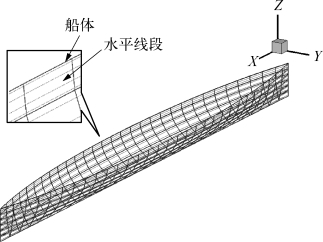
图5.15　WigleyⅢ船体网格划分及面元离散

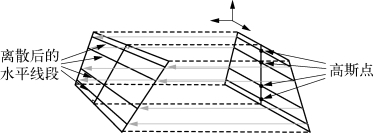
图5.16　面元离散方法

目前工程上常用的势流理论计算有航速船舶的水动力问题的近似方法有两种：一是切片理论；二是在求解边界积分方程时，用无航速的脉动源格林函数代替难以计算的移动脉动源格林函数，并用航速项对水动力系数进行修正（三维脉动源航速修正法，3DP）。这两种方法虽然在理论上与有航速船舶的水动力问题并不完全吻合，但由于其计算效率很高，对于Fr较低的船舶依然可以作为前期设计的有效计算工具。这两种方法的计算结果在这里一起列出，作为计算效果的对比。其中切片理论的结果来自文献［150］，而无航速修正方法的计算结果来自上海交通大学朱仁传研究组开发验证的代码。图5.17～图5.19分别给出了WigleyⅢ船模在三种不同航速下附加质量随遭遇频率的变化。可以看出三种方法在计算船舶附加质量时均能得到与试验较为接近的结果。图5.20～图5.22给出了WigleyⅢ船模在三种不同航速下阻尼系数随遭遇频率的变化。图5.23～图5.25则分别给出了三种航速下垂荡和纵摇的波浪力。

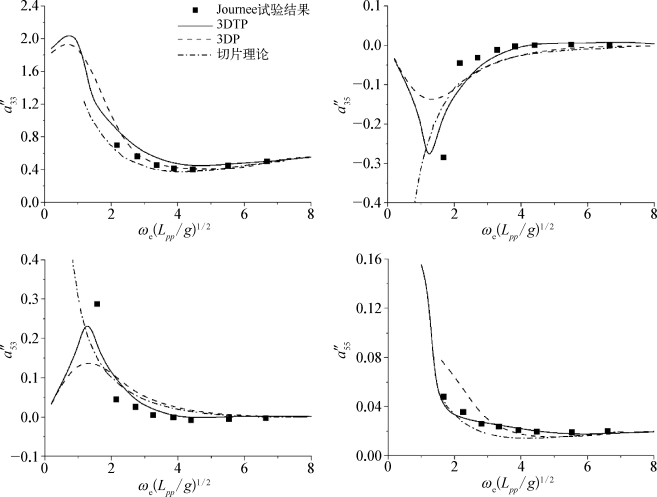
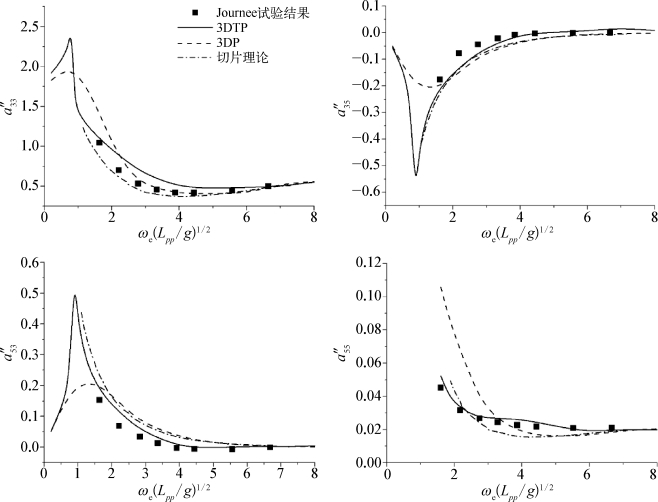
图5.17　Fr=0.2时WigleyⅢ附加质量随遭遇频率的变化（L pp为船型长）

(www.xing528.com)

图5.18　Fr=0.3时WigleyⅢ附加质量随遭遇频率的变化

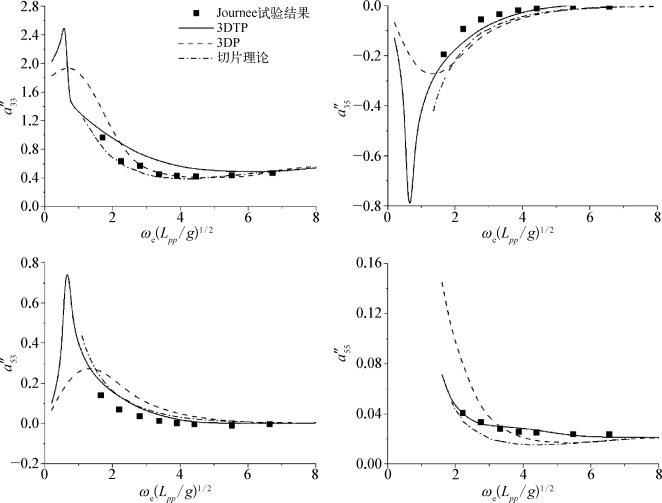
图5.19　Fr=0.4时WigleyⅢ附加质量随遭遇频率的变化

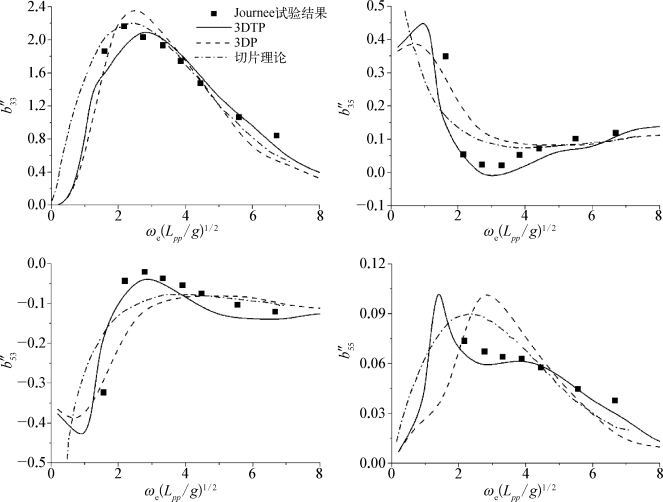
图5.20　Fr=0.2时WigleyⅢ阻尼系数随遭遇频率的变化

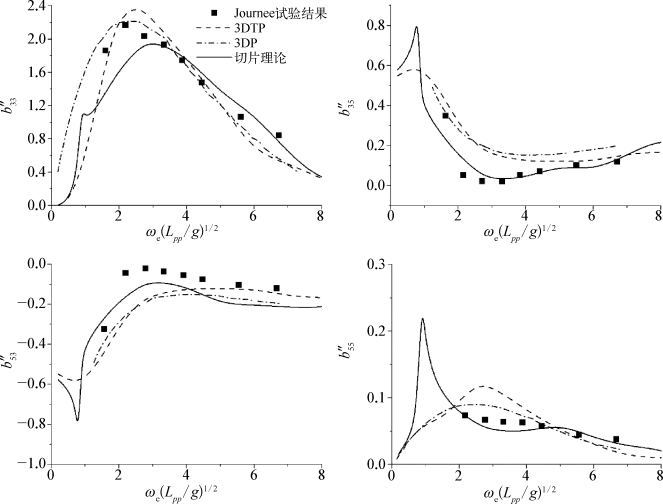
图5.21　Fr=0.3WigleyⅢ阻尼系数随遭遇频率的变化

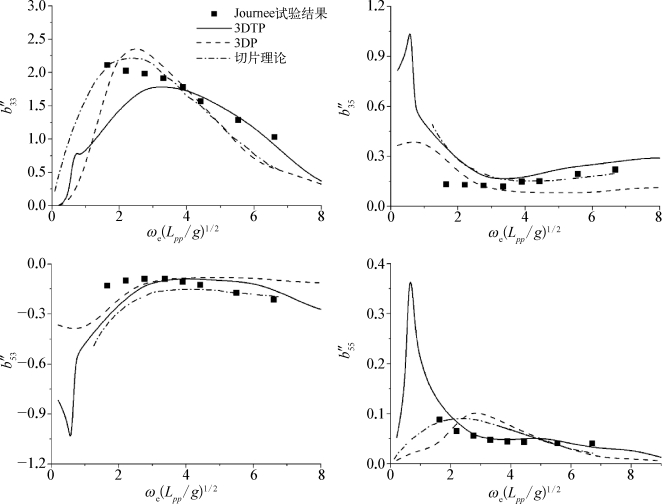
图5.22　Fr=0.4 WigleyⅢ阻尼系数随遭遇频率的变化

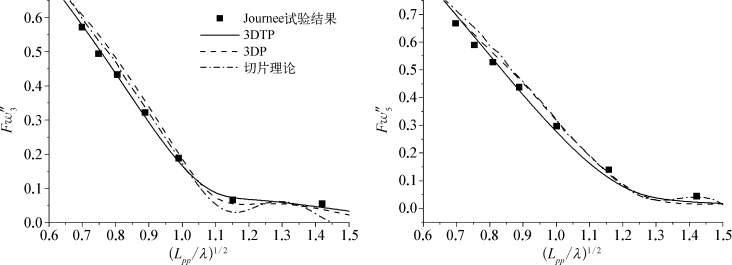
图5.23　Fr=0.2时WigleyⅢ波浪力

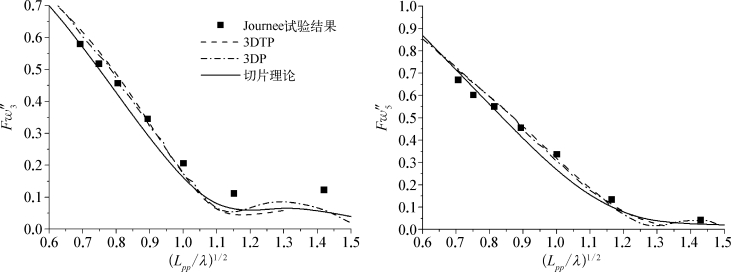
图5.24　Fr=0.3时WigleyⅢ波浪力

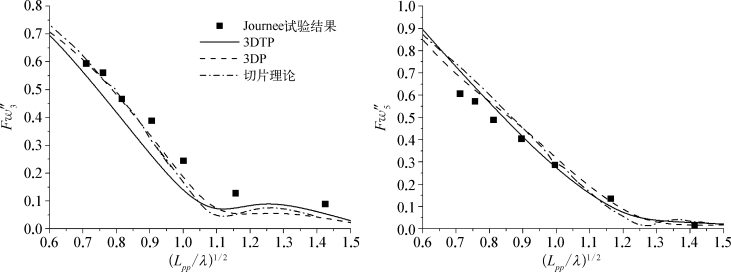
图5.25　Fr=0.4时WigleyⅢ波浪力

通过对比可以看到，三种方法所计算出的附加质量、垂荡和纵摇波浪力均与试验值吻合良好。而在阻尼系数方面，三种方法计算出的B″33、B″35和B″53均与试验的变化趋势相一致，相比较而言，三维移动脉动源法（3DTP）计算出的结果与试验更为接近。而三种方法所计算出的B″55则出现了较大的差别。切片理论和脉动源航速修正法所计算出的B″55均在无因次频率ωe（L pp／g）1／2=3附近出现了峰值，这与试验结果并不相符，而采用3DTP法的结果依然与试验有着很高的吻合度。由此可以看出航速效应对船舶阻尼系数的影响要大于对附加质量和波浪力的影响，尤其是对纵摇模态的阻尼系数的影响最为明显。