格林函数的处理方法-船舶在波浪上的运动理论

移动脉动源格林函数的Fourier二重积分表达难以直接计算，在此基础上，学者们相继推导出了Havelock型、Bessho型和Michell型的表达。其中，Havelock型的单重积分形式非常便于计算，同时有着清晰的物理意义。本节以Havelock型移动脉动源格林函数为例，简要介绍格林函数的数值计算处理。

在式（5.79）及其后续相关的讨论中，对形如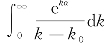的表达进行积分变换，可以将式（5.79）中关于k的积分转化为复指数积分外加留数的表达，从而将双重积分转换为单重积分。其表达形式如下：

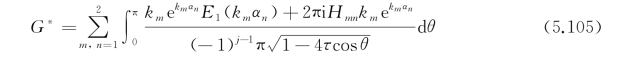
式中，复指数积分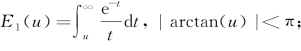；α1和α2的表达如下：

H mn为控制因子，根据不同积分路径的选择其取值也有所不同，本书作者根据许勇等［144］的推导，修正了部分错误，最终表达如下：

获得了G*的单重积分表达后经过简单的运算便可获得其偏导数的表达：

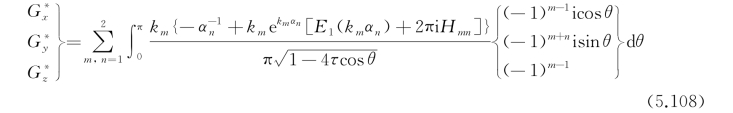
通常可以采用自适应的积分方法来计算格林函数及其偏导数的积分，为了准确计算三维移动脉动源格林函数的单重积分值，需要很好地处理以下几个问题：

（1）θ→ν时，分母（1-4τcosθ）→0所产生的奇异性。

当ν≠0时，积分区间被划分为［0，ν］和（ν，π］两个部分，在前者的右端和后者的左端，θ→ν造成了（1-4τcosθ）→0，使得ν附近的积分精度难以保证。为了提高计算精度可以采用LOBATTO法则来消除积分区间端点处的奇异性，LOBATTO法则表述如下：

式中，余项，n为积分区间离散的数目，若f在［a，b］上黎曼可积，则当n→∞时∣R n∣→0，这样三维移动脉动源格林函数的单重积分可离散为下式：

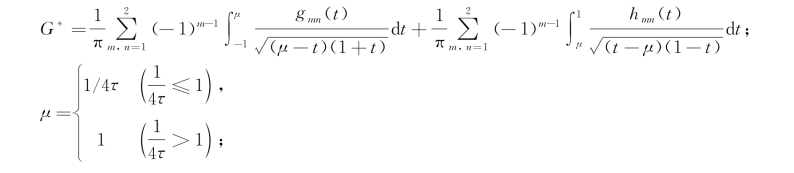
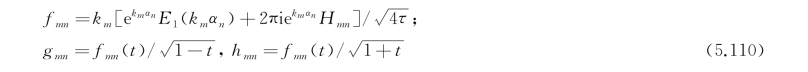
LOBATTO法则用除积分区间两端点外离散点的函数值加权叠加从而近似计算出函数的积分值，这样可以避免了θ→ν时被积函数的奇异性。

（2）复指数积分E 1（u）的计算。

在G*的表达式中含有复指数积分，通常可以用级数展开或者制表插值的方法计算其值，但是级数展开的方法效率低下而制表插值方法的适用范围有限制，故需要更好的求解方法。Hess、Smith［145］给出了利用分式多项式来计算复指数积分的方法：

表5.1　复指数积分比较

(www.xing528.com)

式中，γ=0.577 215 664 9为欧拉常数，M、N、D中的各项系数如下：

Hess、Smith指出：对于0＜|Z|＜∞，其余项|ε|＜7×10-6，表5.1给出了应用分式多项式计算出的复指数积分值和文献［146］给出的解析解的比较，可以看出该方法有很高的计算精度，同时多项式的形式大大提高了计算效率。

（3）θ→π／2时，k 2→+∞使得被积函数成为高频振荡函数所造成的积分困难。

当θ→π／2时，k 1，k 2的表达式分母趋近于0，图5.9给出了k 1，k 2在区间［0，π］上的变化特征。可以看出π／2为k 2的无穷间断点，为k 1的可去间断点，为了消除在实际数值计算中，由于分母过小产生的误差，可以做如下变换：

令，则，将上式带入式（5.82），有

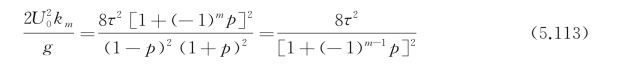
这样可以获得连续的k 1的值，下面讨论k 2→+∞对格林函数积分的影响。G*的表达式中可以看出与k 2相关的项有两项，即E 1（k 2αn）及k 2e k2αn。对于复指数积分，k 2αn是作为积分下限存在的，k 2→+∞使得E 1（k 2αn）→0，故不会对格林函数的积分产生影响；对于k 2e k2αn，由于在实际计算中z，ξ均为小于0的实数，则有

由上式可以看出在G*的计算中，k 2→+∞不会对积分过程有影响。在G*偏导数的计算中，由其表达式可以看到，-这一项的存在使得单独计算其积分值时必然在k 2→+∞时产生奇异性，此时考虑分子中的前两项，有

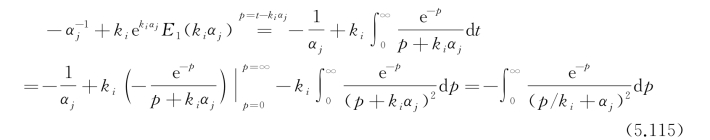
当k m→+∞且p∈［0，∞）时，∣p／k i∣在后续的积分中可以得到有限值，之后可以采用Guass-Laguerre积分来近似获得积分的值。

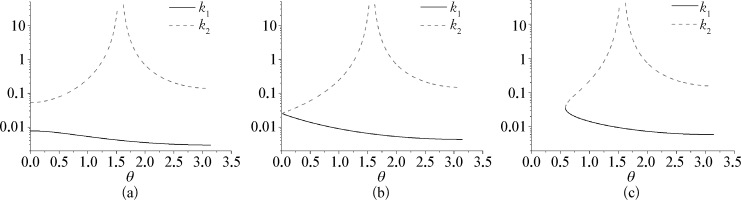
图5.9　不同Brard数下k m的特性

（a）τ＜0.25；（b）τ=0.25；（c）τ＞0.25

洪亮等采用上述方法计算给出了相关格林函数及其偏导数，并与文献进行了比较考证。设源点坐标为（0，0，-1），场点坐标为（x，0.5x，0）且x∈［-12，12］，图5.10是脉动频率ω固定为1.4 rad／s，在移动速度U分别为1.1 m／s、1.5 m／s、2.0 m／s时三维移动脉动源格林函数及其偏导数值［147］。此文献方法的计算结果以实线表示，文献［148］（Inglis＆Price）的结果以符号显示，从图中的比较中可以看出相应吻合得良好。

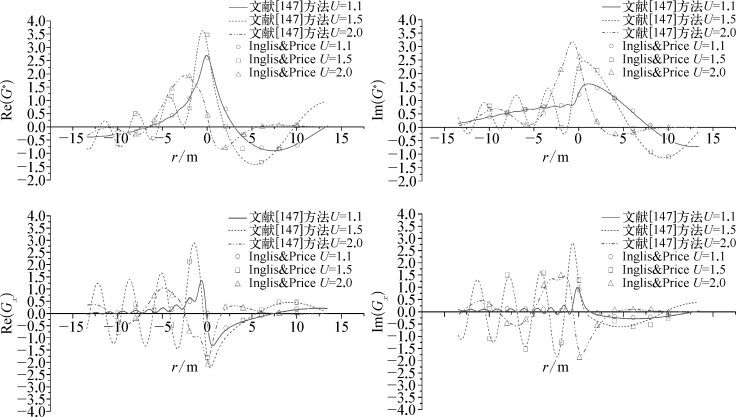
图5.10　不同航速下格林函数及其偏导数

由5.5.3节可知，在获得了三维移动脉动源速度势之后，可计算出其自由面的波形。文献［147］给出了移动脉动源的波纹图，对应于不同Brard数，特别是在τ＜0.25、τ＞0.27以及0.25～0.27这三个区间，波形特征非常明显，体现出不同的物理意义。图5.11给出τ=0.22、0.26、0.68时，t=0时刻计算得到的移动脉动源的波纹。移动脉动源的波纹是由辐射波和移动波叠加组成的，当τ=0.22时，辐射波呈环状，由于源点本身具有x轴正方向的速度U，其波纹在源前较密，源后较疏，同时可以说明此时辐射波的传播绝对速度大于点源移动速度；当τ=0.68时，源点前方无波，在源点后方存在辐射波和移动波，环状的辐射波只限于某个楔形角内，此时辐射波的传播速度小于点源移动速度；τ=0.26处于前两者的过渡状态。图5.11与前述分析一致。

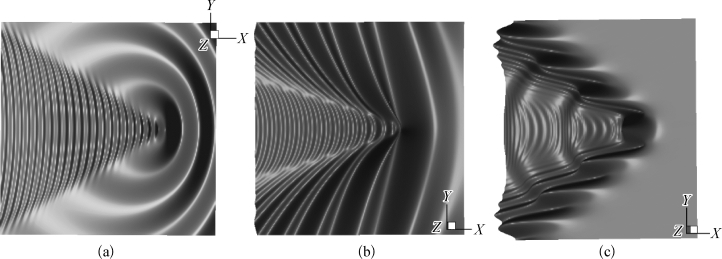
图5.11　三维移动脉动源波形

（a）τ=0.22；（b）τ=0.26；（c）τ=0.68