船舶波浪运动理论-方程离散化与求解

与有航速规范化辐射势的源分布计算式（5.74）推导方法一致，采用内场开拓的方法，很容易获得无航速规范化辐射势式（5.14）对应的源分布计算式：

根据第2章（2.2节）可知，决定源强σ（Q）的积分方程为

式中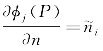，由物面条件提供，是已知的。该方程可在离散化后，化成代数方程组求解。离散化的一种做法是将物面S 0分成小块面元，如分成N块，设每一块面元上分布等强度的源，即在标号为n（n=1，…，N）的面元上，σn为常数；并且在每一块面元上选一控制点P n，在这些离散的控制点上满足边界条件。于是，积分方程（5.101）就离散化为一组线性代数方程组：

一旦控制点P n确定，即可求出上式中面元ΔS i上的积分，其中Qi是面元ΔS i上的点。如把上式写成矩阵形式，有

式中，［H］为阶N×N的矩阵，由上式中σi前的系数所组成；｛σ｝为欲求源强的N阶列阵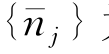；为单位法线矢量对应于j模态运动的分量所组成的N阶列阵。这一矩阵方程的解为(www.xing528.com)

对于各种不同的运动模态，矩阵［H］是相同的，常称作影响矩阵，它只与物体形状、分块大小和形状及控制点的选取有关。一旦其逆矩阵求得，由简单的矩阵乘法即可获得不同运动模式时相应的源强分布，从而确定场内各点（包括物面）的速度势。

上述的求解方法常称为局部适合法（collocation method），也称面元法（panel method）。通常将物面分成四边形面元的组合。在计算开始的输入数据中，四边形的四个角点是物面上的型值点。这四点往往不在一个平面上，为便于求得面元ΔS i上的积分，须用某个平面单元来取代实际的曲面元，因四点不在一个平面上，故平面面元常取成平均平面。这样，两个相邻平面面元间可能会出现缝隙，物面的近似“棱角面”是不连续的。同时，现在面元上的法线矢量n严格来讲已不再是物体表面的单位法线矢量，而是平均平面元上的单位法线矢量了。此外，如离散化时所假设的那样，每一面元上的源强分布是常数，则面元之间源分布是不连续的，是有阶跃式的不连续性。但尽管如此，当面元数目N足够大，即物面分割得足够密时，上述离散化方法能给出相当满意的结果。

采用面元法离散求解有航速情况下的源分布边界积分方程式（5.74），还需要在水线上布置相应的线段源。这里求解方程［见式（5.101）］得到的只是边界上的源强，还需要通过式（5.100）或式（5.74）积分计算获得边界上离散点源的速度势。类似地，离散面元计算法也可以应用到直接求解方程式（5.14）和式（5.71），获得的解即是边界上的速度势。因此，对于求解速度势来说，前一种方法常被称为间接法，后者则谓之为直接法。

由式（5.102）可以看出，面元上的源强分布已假定是常数。若面元上的速度势分布可以用面元顶点处的速度势线性表达（即面元上的速度势线性分布），那么面元之间的源分布是连续的，导数还不连续。当面元上的速度势被考虑为二阶或更高阶函数分布的话，甚至是非均匀有理B样条函数分布，则面元之间的源分布及其导数都是连续的。根据面元上速度势分布函数，相应的数值离散计算方法称为线性面元法、高阶面元法。