船舶波浪上运动理论验证

已经看到，当船舶一面以平均前进速度前进，一面作简谐振荡运动时，场内辐射势可以由式（5.74）确定。另外的关键是求解格林函数G（P，Q），其中P坐标（x，y，z），Q坐标（ξ，η，ζ），它们均在以船舶平均前进速度（航速）U 0移动的参考坐标系中度量。格林函数G（P，Q）要满足的定解条件是

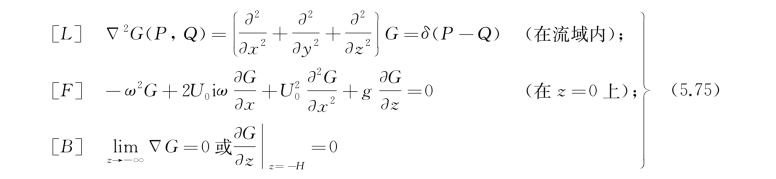
式中，δ（P-Q）为狄拉克δ函数，底部条件［B］的前一式适用于无限水深的情况，后一式适用于有限水深且水深均匀、深度为H的情况。除上述三个条件外，还需附加合适的辐射条件，这将在后文中加以讨论。

与三维脉动源定解条件类比可知，移动脉动源问题的主要差别在于自由面条件［F］，它可视为一脉动源有移动时在参考坐标系中须满足的自由面条件。

事实上，假设一个脉动源，沿x方向以等速U 0移动，经过相当长时间后，整个流场的运动已达到稳态。若从以速度U 0移动的参考坐标系oxyz中考察这一移动脉动源引起的速度势Φ（P，Q，t）≡Φ（x，y，z；ξ，η，ζ），其中Q（ξ，η，ζ）为源点，P（x，y，z）为场点，则Φ要满足的自由面条件为

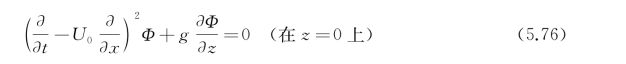
构造速度势形式为

式中，ω为脉动圆频率，Re指取表达式的实部，下标R和I分别表示某一量的实部和虚部。将Φ代入式（5.76），易知G须满足的自由面条件就是式（5.75）中［F］。

按源函数的性质，对无限水深的情况，设

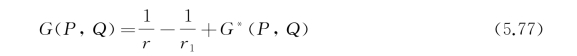
式中，r 2=（x-ξ）2+（y-η）2+（z-ζ）2，r 21=（x-ξ）2+（y-η）2+（z+ζ）2，G*（P，Q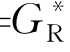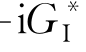）=+在z＜0的下半空间内是调和的。为了求解G*（P，Q），与静止脉动源求解的做法类似，可从自由面条件入手。应用已经证明的积分关系式：

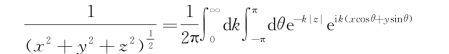
可将1／r和1／r 1表示为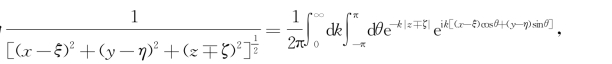从而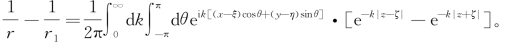

其中因在定义域中z＜0，ζ＜0，故

关于固定的源点，自由面条件是在z=0上满足的，故在自由面条件中取前一个等式。

鉴于，按式（5.75）中的［F］，可得G*（P，Q）要满足的自由面条件是

或记作

显然，可以设G*（P，Q）具有形式

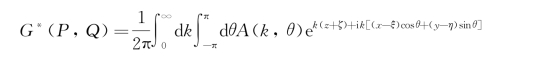
将其代入式（5.78），得　

于是

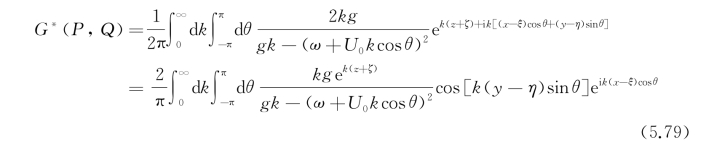
现在的问题是如何给这个积分以合理的解释，以消除积分核中奇点所造成的困难，同时满足适当的辐射条件保证解的唯一性。为此需要分析该积分核中分母的零点。该积分核中分母可写成

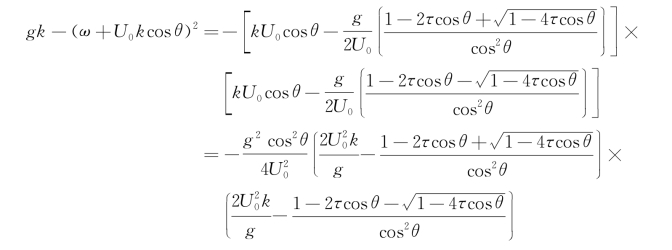
式中，τ0=U 0ω／g。显然，上式的零点为

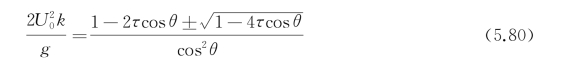
如果4τcosθ＞1，k 1，2是复数，零点不在实数的k轴上，上述积分核无奇点。

定义实数ν为

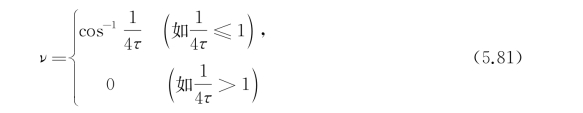
显然，ν介于0与π／2之间。若4τcosθ＞1，cosθ＞cosν，即0≤θ＜ν时，积分核的分母无实数零点。而ν＜θ＜π时，式（5.80）有两个实根，其中当时，有一根趋于无穷大，另外，在此区间中，1-4τcosθ＞0，1-2τcosθ＞0，且

故两个根是不等的正根，如图5.3所示。

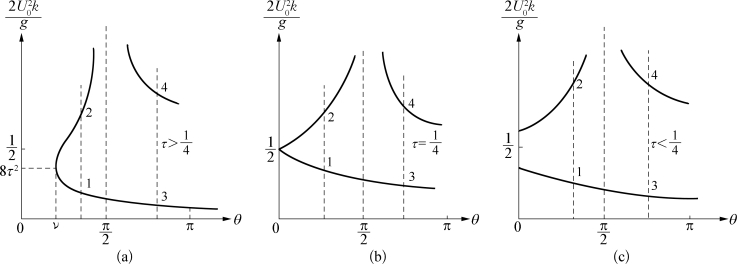
图5.3　式（5.80）的根

为区别起见，记

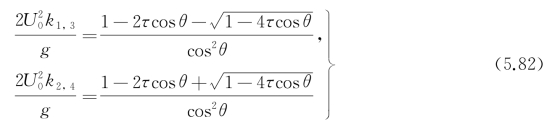
式中，k 1、k 2是θ在［ν，π／2］间的两个根；k 3、k 4是θ在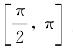间的两个根。

式（5.82）又可改写为

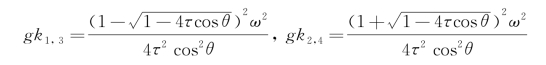
两端开方，取其正根，则有

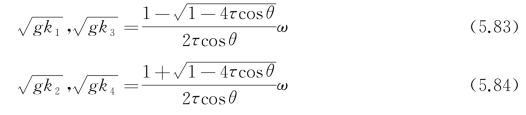
这样G*（P，Q）可写成

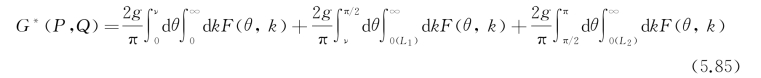
式中，右端第一项是本义积分，第二、三项的积分核各含两个奇点k 1、k 2和k 3、k 4，需要解释才有意义。式中F（θ，k）定义为

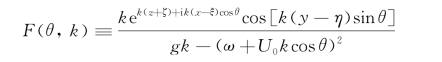
如图5.4所示，求解式（5.85）中积分时，若积分限在间，取积分路径L 1；当积分限在　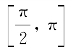间时，取积分路径L 2。

图5.4　格林函数积分路径

上述积分路径的选取就是对积分的一种解释，它是唯一能满足辐射条件的选择。下面来探讨一下按所选路径积分后，解满足的辐射条件。

将被积函数F（θ，k）中的分母改写为

这里θ限于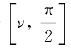之间。如果θ在之间，则应将k 1改为k 3，k 2改为k 4。于是

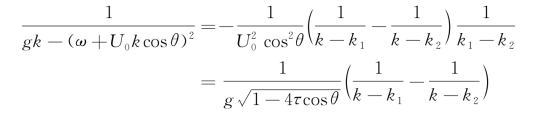
则G*（P，Q）中的第二项变为

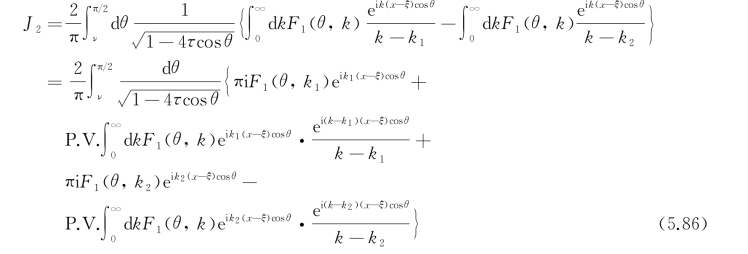
式中，F 1（θ，k）≡k e k（z+ζ）cos［k（y-η）sinθ］，P.V.是积分取柯西（Cauchy）主值的意思。应用前一章中曾采用的傅里叶积分定理，若f（x）在［a，b］内是一致连续的，则当t→∞时，

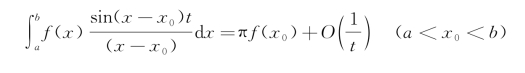
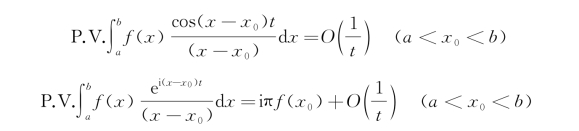
可以得到J 2的渐近形式，在x→+∞时，

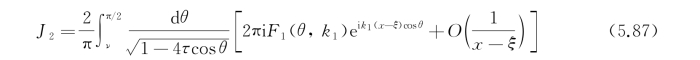
在x→-∞时，(https://www.xing528.com)

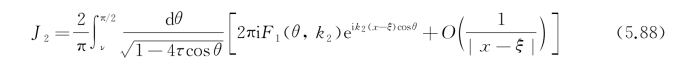
由于G*和振荡因子e-iωt是一起出现的，积分路径L 1的选择使得J 2的贡献是：物体的远前方（x→+∞）只有波数为k 1的波和物体运动同向传播，而在物体后方（x→-∞），只有波数为k 2的波与物体运动同向传播。

考虑θ介于　间的情况：

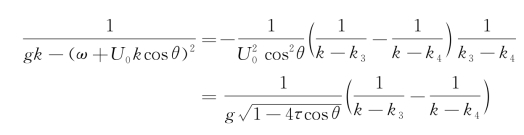
G*（P，Q）中的第三项积分可以写成

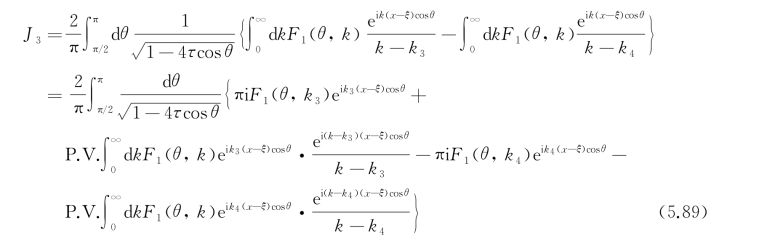
再次应用前述的傅里叶积分定理，不过要注意到现在cosθ＜0，于是，在x→+∞时：

而在x→-∞时：

选择路径L 2积分的结果是，J 3的贡献：在x→-∞时，有两个波数分别为k 3和k 4的波逆物体运动的方向传播；在x→+∞的远前方无波浪出现。若改变积分路径L 2的选择，将会在物体的远前方出现逆物体运动方向传播的波浪，这违背物理现实。

现在说明θ介于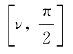之间的两个与物体运动同向传播的波系。由图5.5可见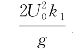，对应的波数k 1小，波长大，传播得快，但要出现在物体的远前方，其传播速度必须比船速U 0大；反之，与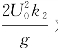对应的波数k 2较大，波长短，传播得慢，但要在船的远方出现而仍和船同向传播，其传播速度必然要比运动速度U 0小。事实上，对固定的τ，从图5.3可知，恒有

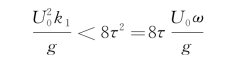
或者

另一方面，从所选择的θ范围ν≤θ＜π／2看，cosθ＞0，要求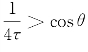，故有

式中，ω／k 1是波速（又称相速），前一式表明，波速比船速在波速方向的投影U 0cosθ大；后一式可理解为：与U 0成θ角传播的波浪，它在U 0方向的“有效”波速ω／k 1cosθ比船速快（见图5.5）。

对于k 2，由式（5.92）和图5.2可知：

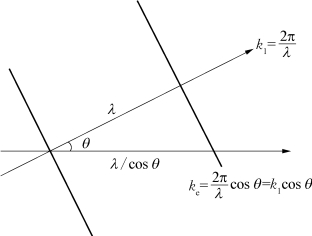
图5.5　波数k 1和“有效”波数k e

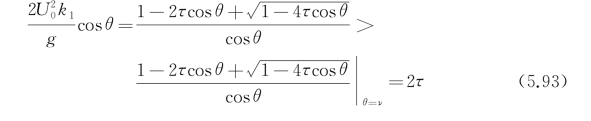
即

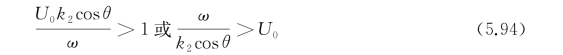
总之，当物体以等速移动并作简谐摇荡时，只有那些与物体同向而传播速度又快于物体的波浪方能在远前方出现；而那些在物体远后方的波浪，要么与物体逆向传播，要么以低于物体移动速度的速度与物体同向传播。

将式（5.86）和（5.89）加以合并，G*（P，Q）的表达式（5.85）又可写成

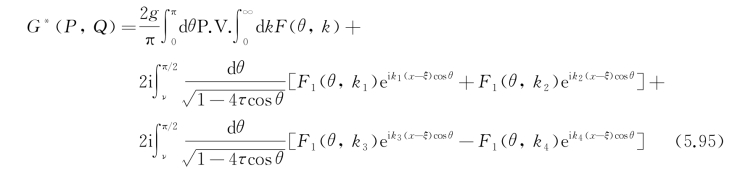
它的渐近式，根据式（5.87）～（5.91）应是

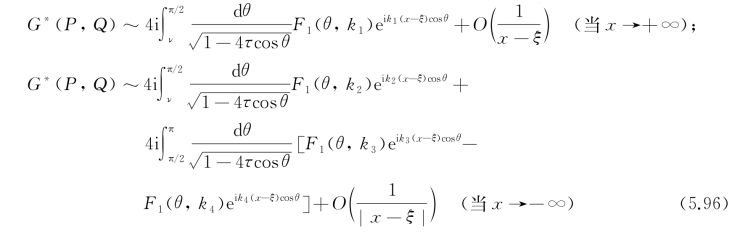
5.5.3　移动脉动源的波形

移动脉动源产生的波浪，既不同于纯移动源的兴波，又与纯脉动源（静止的）的波形极不相同。前者是著名的开尔文（Kelvin）波系，在船前无波，在船后的一个楔形地带内出现横波和散波；对于深水情形，楔的半角Θ为19°28′。后者是简单的环形波，向四周均匀辐射。两者的远方的渐近解中都只有一个波数出现。深水时，移动源兴波的波数是k=g／U 20cos2θ，脉动源辐射波波数是k=ω2／g。对移动脉动源来说，远方渐近解中出现了一般互不相等的四个波数k 1、k 2、k 3和k 4。

从原则上讲，既然得到了移动脉动源速度势的远场渐近解，其远场波形可由

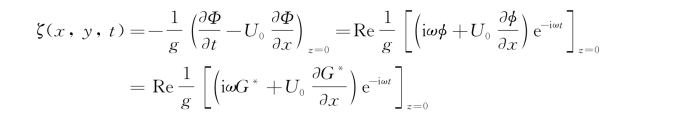
决定。G*（P，Q）由x→±∞的渐近解（5.96）给出。

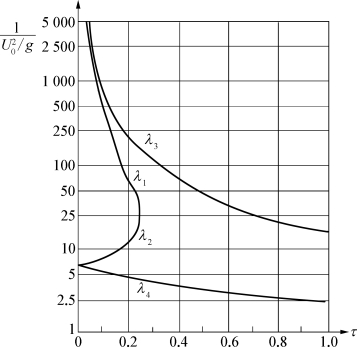
图5.6　波浪长度随τ的变化曲线

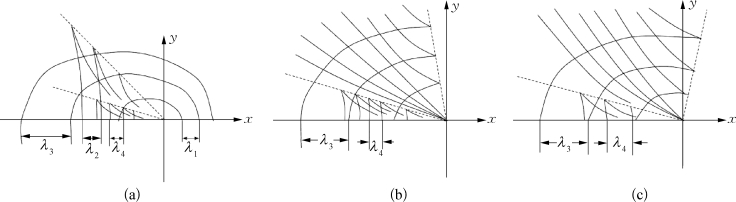
图5.7　移动脉动源的波纹图

（a）τ＜0.25；（b）τ＞0.27；（c）0.25＜τ＜0.27

图5.6是倍克（Becker）［142］计算的在x轴上的波浪长度随参数τ=U 0ω／g变化的曲线。在时，对固定的τ，沿x轴有四个不同的波长，其中λ1和λ3是环形辐射波的波长，λ2和λ4是某种移动波的波长。在时，只有两种波，其波长分别为λ3（辐射波）和λ4（移动波）。图5.7是对应的移动脉动源的波纹图［142］。图5.7（a）是时的波纹，由图可知，辐射波呈环状，由于源点本身向前移动，故波纹在源前显得密些，在x轴上截取的波长是λ1；源后显得疏些，在x轴上截取的波长是λ3。同时，环状不再是圆形，而约略呈椭圆状。并且，既然源前有波，这种辐射波在x轴正向传播的绝对速度必然大于源点移动的速度U 0。此外，图中还显示出两个类似开尔文波的波系，一个夹角（2Θ）大些，一个夹角（2Θ）小些，在x轴上截取的横波波长各为λ2和λ4。根据上节的讨论，这两个波系中一个应该随源同向传播，但波速比U 0小，一个应该逆向传播。图5.7（b）是τ＞0.27时的波纹，这时源前的波消失了，环状的辐射波只限于某个楔形角内。沿x轴截取的波长只有两个，一个是λ3，逆向传播；一个是λ4，随源同向传播，波速比U 0小。

由图5.7（a）和（b）可以看到，两个开尔文波系的楔形角2Θ是随参数τ而改变的，图5.8是莱特希尔（Lighthill）［143］给出的半楔角Θ随τ的变化曲线。当τ=0时，Θ等于开尔文波纹的半楔角19°28′。当τ≠0时，恒有两个不同的半楔角Θ，一个大，一个小；小的总是小于19°28′，大的在τ＜1.62时总是大于19°28′。大的半楔角在时是不定的，但在0.25＜τ＜0.27这个小区间内，它是大于90°的，图5.7（c）表示的就是这种情形。

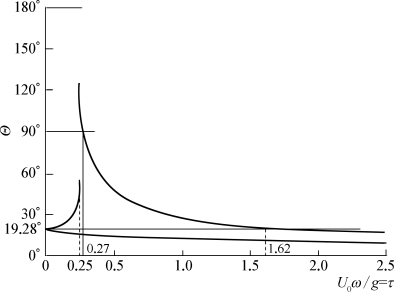
图5.8　平面角Θ随τ变化曲线

船前有波这一事实在进行模型试验时应予注意。如果τ＜0.27，船模前面的这种波［如图5.7（a）和（c）］遇到池壁将反射回来，从而对船模前面的流体施加了不应有的扰动，这也是一种池壁效应。

从前面的讨论可知，参数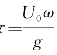起着非常重要的作用，而且在时解有异常的性质。那么，参数τ的物理意义是什么？又是代表什么情况？这些问题我们必须考虑和回答。

在物体边移动边摇荡的时候，有两个无量纲参数影响运动的性质，一个是傅汝德数Fr=，它表征着物体振荡兴波。此处L为船长。两者相乘，得到一个新的无量纲常数，即Brard数，，它与物体移动兴波相联系；另一个是无量纲频率

固定点源振荡兴波的波数是，而频率为ω的相速度C=ω／k 0=g／ω，则参数τ代表移动速度与振荡波相速度C之比，即

显然，τ增大意味着U 0增大或C减小，或者U 0增大得比C快。对照图5.7的波纹不难理解，当τ较小时，向外传播的辐射波可以超过源点而在前方出现；随着τ增大，波浪只能在源后出现，而且其存在的范围被限制在半楔角为Θ（大值）的楔形内。由图5.8知，当τ＞0.27时，半楔角Θ随τ的增大而减小，当τ足够大时（如τ＞1.62），这个半楔角甚至可比19°28′还要小。

从上面的解释来看，也许会认为τ=1是个临界值，因为τ＞1意味着移动速度超过波速。但是，从波浪产生的角度来观察，波前（wave front）是以群速C g（对　深水而言，）移动的，这样临界值似乎应该是。不过，现在物体是边移动边振荡，情况显得更复杂，难以通过上述简单的考虑来解释清楚。然而，从前面关于波纹的讨论中已大体可以猜出，问题的症结是由与源同向移动的两个波λ1和λ2的干扰所引起的。由式（5.82），λ1对应的波数是

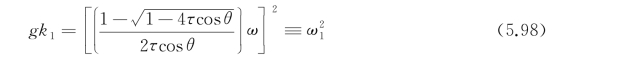
因为波长λ1的波是一种辐射波，故将波数和频率的关系（色散关系）人为地写成式（5.98）的形式。这里引入了所谓的等效频率，这样一来，k 1与ω1的关系就与普通静止脉动源的色散关系一致了。同样，对波长为λ2的波有

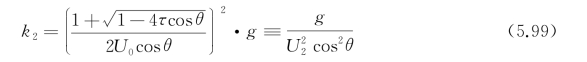
因为这个波像移动兴波，故引入等效速度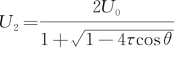之后，k 2与U 2的关系就与一般移动点源的关系一致了。则

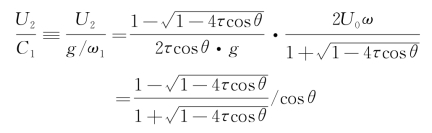
若θ=0，则cosθ=1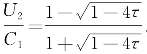，。由此可见，如。移动波系的速度U 2和辐射波系在正前方（θ=0）恰好相等。如果从波能移动的角度来看，它们的波群速也是一致的。不要忘记，这里的兴波是由源点的移动和脉动引起的，能量不断地从源点输入波浪，这两个波系的能量就不断地堆积在一起，且已经过了无限长的时间（因为已假定是稳态的）。

这个问题还可从固定坐标系来观察。在动坐标系中波数为k而振荡频率为ω的波浪转换到固定坐标系后，有效频率ωe=U 0k+ω。由

可以看出，这完全是一个在固定坐标系中的波浪传播问题，相应的波速

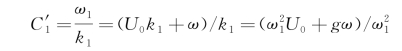
式中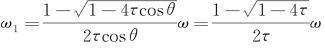，（若θ=0，cosθ=1）。将此关系式代入，得

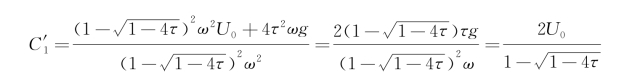
十分明显，若是向前传播的振荡波的波速，它的群速是，故C′g=U 0。这就是说，在固定坐标系中来考察的话，物体振荡不断地产生波数为k 1的波，它的能量沿物体正前方传播的速度，正好是物体移动的速度，经过长时间的积累，奇异现象自然产生。

当然，这里所有的讨论都是基于线性理论的。实际上，在“奇异现象”发生之前，非线性效应早已出现，故不一定会实地观察到这一奇异性。