船舶波浪上的运动理论+格林函数解法

上一节讨论了有航速时船体摇荡辐射势的定解问题构成和它的分解。对于各运动模态j=1，2，…，6，规范化辐射势φj的定解问题应是

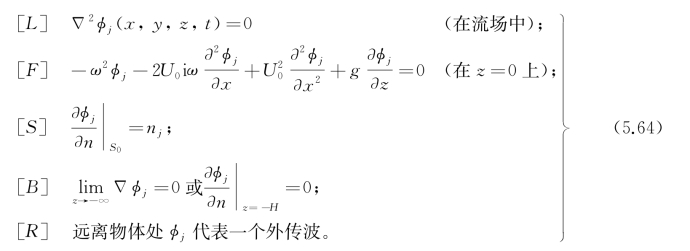
上述定解问题与无航速情况相比，唯自由面条件更加复杂外，是颇为相似的。由此自然产生的一个想法就是仿效无航速时的做法，引进格林函数：

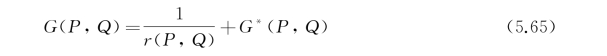
式中，P（x，y，z）为场内某一场点，Q（ξ，η，ζ）为源点为P、Q两点的距离，G*（P，Q）为场内的调和函数。令这一格林函数在P≠Q时，满足式（5.64）中除物面条件［S］外的其他所有的定解条件，试图将场内任意点P上的速度势用这一格林函数及其法向导数在物面上的分布表示出来。事实上，从下面的推导结果可以看出，这时除了上述的物面分布外，还多出一项沿静止水线面的积分，其原因是即使φj和G在由面上满足同一条件，自由面上的积分也不能像无航速情况那样正好抵消掉。

满足要求条件的格林函数（5.65）是可以找到的。在下一节专门讨论这一问题，为方便起见，将其［式（5.65）］略加变形，记为

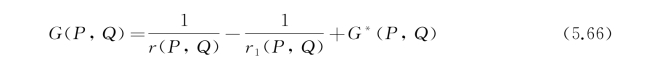
式中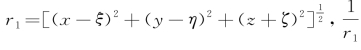和G*在z＜0的下半空间内均是调和函数。G（P，Q）对坐标变量P或Q将是对称的，在G要满足的定解条件中将变量x、y、z与变量ξ、η、ζ对换也无不可。这一点在下一节G（P，Q）的表达式中可以清楚地看到。

现在转而讨论场内势函数的表达和求解。仍考虑由平均物面S 0、自由面S F、半径R为无穷大的垂直圆柱面S R及池底S B（z=-H，或H→∞）所围成的流域。由格林第三公式，场点P（x，y，z）上的辐射势φj（P）可写成（略去下标j）

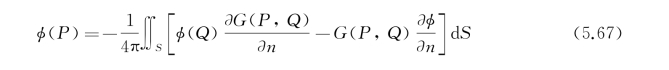
式中，指函数在流体边界上的法向偏导，单位法线矢量n指向流体外部，S=S 0+S F+S R+S B。

不难看出，由底面上φ和G满足的底部条件，沿S B的积分实际上并不存在。在无穷远处的辐射圆柱面S R上，根据以往关于三维脉动源的经验，完全可以假定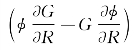沿S R

的积分在R→∞时趋于零。于是式（5.67）退化成

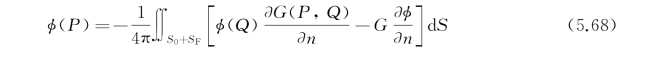
在S F面上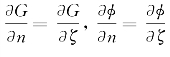，积分号内φ（Q）=φ（ξ，η，ζ），它满足的自由面条件是在ζ=0上

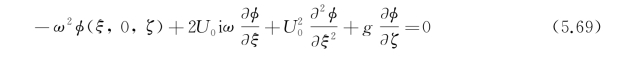
而G（P，Q）=G（x，y，z；ξ，η，ζ）中P、Q的关系是以（x-ξ，y-η，z±ζ）的形式出现的，且在G*（P，Q）中无z-ζ形式出现。注意现在场内变量仍是x、y、z，只不过在式（5.68）右端的面积分中对每一选定的场点把（x、y、z）视为固定量（参量），把边界上的源点Q（ξ、η、ζ）视为积分变量。故而在自面上，有正好在形式上就是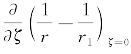（以z替代ζ）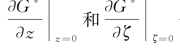

也是如此，故G（P，Q）在ζ=0上满足的条件为

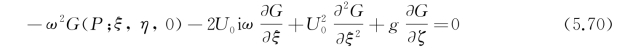(www.xing528.com)

这与对称性的叙述并不相悖，当我们提及对称性时，意味着场点与源点事实上的对换，而现在情况并非如此。

将式（5.69）和（5.70）代入积分式（5.68），可见沿自由面的积分为

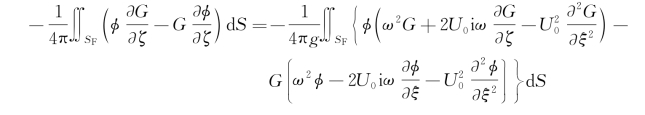
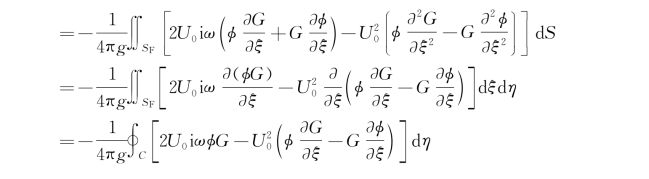
上式最后一步中已根据G和φ在远方的性质，略去了沿半径的圆周上的线积分，式中C为船体与静水面的交线，即水线（见图5.2）。于是式（5.68）变为

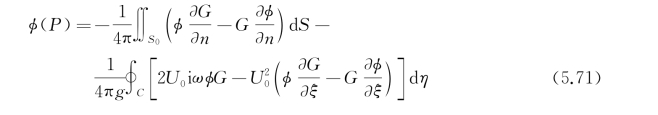
其中沿水线C积分时，积分路线走向与垂直轴成右手定则。对水下物体或者U 0=0的情况，线积分项消失了。在船体不产生振荡时，ω=0，式（5.71）简化为众所周知的诺埃曼　开尔文问题（Neumann-Kelvin problem）。与此对应，目前讨论的这类问题叫作诺埃曼-哈斯金特问题（Neumann-Haskind problem），以纪念第一个推导出这个格林函数（如下一节所述为移动脉动源）的哈斯金特［8］。

由式（5.71）可见，速度势φ（P）是由分布在船体湿面积S 0和水线C上的源和偶极子所形成的。在S 0上偶极子方向沿物面的法线方向；在水线C上不管C的形状如何，偶极子总是沿着ξ轴的方向。这两类奇点的分布，可借助流场向船体内开拓，并构造一个内域解的办法消去其中的一种。

把式（5.71）当作外域解，并记以φ（e），当把它应用于内域时，左端是零。类似地，构造一个内域解，记φ（i），可写成

将它应用于外域时：左端也是零；式中第一个积分式前与式（5.71）差一个符号，这是因为此处的法线方向改变了，与式（5.71）中的一致了；第二个积分号前符号不变，是因为该处的指向流域外部的法线方向正好与外场一致（即与ζ指向一致），唯线积分路径走向与式（5.71）中的相反，正是由于这种走向保证了以C为边界的自由面保持在曲线走向的右面。将两式（即内、外域解）相加，并改变线积分的走向，使式（5.72）中的走向与式（5.71）一致，于是有

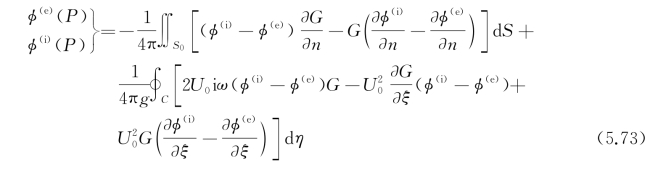
保留源分布而消去偶分布时，在S 0上令

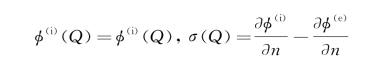
于是流场中任意点P（不管是内域或外域）的速度势可写成

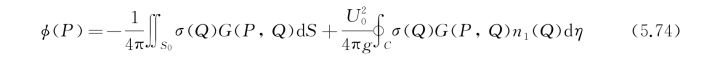
式中，σ（Q）可认为是源强分布密度，n 1（Q）是水线C处物面单位法线矢量在ξ轴上的分量。n 1（Q）的出现是由于定义，而沿水线C的线积分中出现的是，这里取，原因是内外域的解沿曲面S 0是连续的，且φ（i）=φ（e），只有法向是间断的。

式（5.74）中的未知函数（源强）σ（Q）由物面条件［S］决定，不同的运动模态对应有不同的源强分布，但它们均可化成相同类型的积分方程，不同者只是右端项n j而已。应用这个计算办法的包括张及英格列斯和帕莱斯［140，141］的工作，由于此方法的复杂性和费时性，到目前为止还未曾广泛应用。在上述推导过程中，除了应用定常兴波势和辐射势都是小量的假定外，不曾采用其他假定。然而，定常兴波势是小量的假定，暗含着对船体形状的限制（此处不考虑深潜或低速情况），这一限制或隐含假定在以上推导过程中不曾用到。

解出φj后，应用上一节的公式，即可求出船体附加质量、阻尼系数和相应的辐射力。