航行船舶的辐射问题解决方案

由前面几节可以看出，在势流理论范围内，无航速时辐射势的一阶近似问题可以大致认为已经解决，即应用格林函数法可求得扰动势的解和物体的受力。在船舶有航速的情况下，仅假定物体摇荡兴波小是不够的。如第4章所分析，尽管在摇荡兴波是小量的假定下，对摇荡速度势来说定解问题也可以是线性的，但其中自由面条件式（4.36）过于复杂，而且出现了定常兴波势的耦合影响，它必须通过定常兴波势的非线性定解问题的求解来确定。因此，目前比较现实的做法是进一步假定船体的定常兴波也是小量，这时，定常兴波势与摇荡速度势的耦合影响可以忽略，从而使摇荡速度势本身的求解独立。要满足船舶定常兴波是小量的假定，必须要求船体要么窄，要么细长；或者船可能是个潜体，且有一定的潜深，或者船速可能较低。深潜假定曾被海夫洛克广泛采用［127］，但这时船舶在波浪中摇荡的矛盾也缓和了，且这种假定仅适用于特殊类型的船种。低速船假定或“慢船”假定在兴波阻力理论中是个时髦的课题［136］，但其在波浪上运动的研究中尚未见有人采用。在密契尔（Michell）的兴波阻力理论启发下，窄船假定应用于运动问题是最自然的［137139］，但窄船作垂荡运动时，引起的流体动力扰动大小，与试验结果不符。彼得斯（Peters）和斯托克（Stoker）曾引进扁船假定，但其中也有不少理论上的困难，其应用仅限于无航速的情况［138］。目前来看，细长船假定最有希望，讨论也比较多［15，127］。

本节将在细长船的假定下，在三维流动的意义上处理有航速时船体摇荡的辐射问题。由细长假定而来的进一步简化（切片近似）将留待后续章节中讨论。

在4.5节中已讨论，当船舶有前进速度且作摇荡运动时，即使摇荡是个小量，场内不定常速度势Φ（x，y，z，t）满足的定解条件可以线性化，其理论分析仍是非常复杂和难以奏效的。参见式（4.62），其中最主要的困难在于定常航行兴波与摇荡兴波的耦合影响。为避开这一困难，需要进一步引进定常兴波也是小量的假定。由于船舶往往具有细长的外形，细长假定有一定的现实基础。在细长体及定常兴波是小量的假定之下，定常兴波与摇荡兴波在一阶近似中可以看作是完全独立的。此时，若仍考虑辐射问题而不计入射波，则场内摇荡辐射势ΦR（x，y，z，t）满足的定解问题应为式（4.64）。将这一定解问题重新写出来，为简洁计，略去表征辐射势的下标R，则辐射势Φ满足的定解问题为：

当然，上述定解条件是在与船体一起平移的参考坐标系中表达的，其中U 0是船的前进速度，ξj为船体摇荡运动的广义位移。

考虑船体摇荡是简谐运动的情况。这时船体摇荡的广义位移可记为

仿效前面速度势分解的做法，相应地令

上式的实部是我们所要的有物理意义的解，其中空间速度势

以上各式中，φj为相应于某一运动模态的规范化速度势。按式（5.52）的物面条件［S］不难得到在物面S 0上φj应满足

同样，将式（5.53）代入式（5.52）的自由面条件，得φj应满足的自由面条件是

此外，φj应满足类似式（5.52）中的其他条件。与无航速情况相比，在摇荡运动和定常兴波都是小量的双重假定下，唯自由面条件更加复杂，φj（x，y，z）的求解亦可用格林函数法进行，这将在下一节中讨论。现暂设φj（x，y，z）是已知的，进而来阐述这时船体的受力和力的表述问题。

船体受力在参考坐标系轴线上的投影是

而绕通过动坐标系原点O的瞬时轴的力矩在动坐标轴上的投影是

式中，S应是船体的瞬时湿面积，在小振荡运动的假定下，它与参考系中的平均湿面积的差别是小量，中包括了定常兴波的影响，在定常兴波也是小量的假定下，与静止时的湿面积S 0之差也是小量。

为书写方便，略去x、y、z上的撇号。且限于一阶近似，上二式可用广义力和广义法向矢量统一地记为

式中，p为船体因摇荡而引起的流体动压力，它可根据式（4.65）的第二式由不定常辐射势Φ得出，即

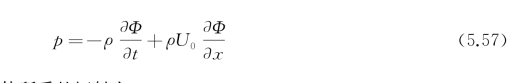
将式（5.57）代入上式，易得船体所受的辐射力：(www.xing528.com)

其中已定义

由式（5.58）可知，μij仍然是附加质量，λij仍然是阻尼系数。但从式（5.59）看，它们关于下标的对称性不再成立，且附加质量矩阵｛μij｝和阻尼矩阵｛λij｝都不再是正定的了。一旦各运动模式的辐射势φj能够解出，由式（5.59）就可得到船体有航速摇荡时的流体动力系数A ij=。在式（5.59）中，积分项中不仅出现φj，还出现，在计算时固然可通过数值微分求得，但精度不高。事实上，如果充分地利用船体细长的条件，含的积分项可进一步用斯托克斯公式变形，并可以与其他项进行量级比较，以决定取舍。

当i=1，2，3时，n=（n 1，n 2，n 3），应用第2章中的斯托克斯公式（2.59），并令V=iφ，则有

如图5.2所示，n是船体表面的单位内法线矢量；C是船体静止时的水线，其走向与S 0的方向成右手定则。由于现在C在xoy平面内，d e=i d x+j d y，故有

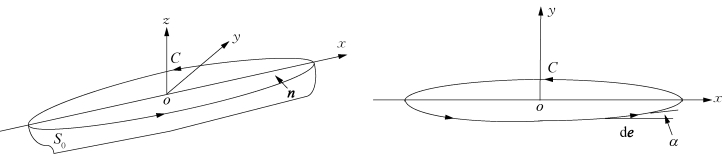
图5.2　船体表面水线

式中，α是d e与ox轴的夹角。在细长船情况下，sinα≈α是个小量；同理，n 1也是小量。故由式（5.60）可得到

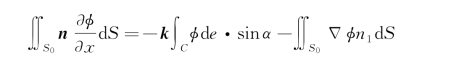
其亦是个小量，或者说，它比要高一个量级，可以略去。

当i=4，5，6时，（n 4，n 5，n 6）=（r×n）。这时要采用第三斯托克斯公式（2.62），其中令V=iφ，易证

将以上各式代入式（2.62），并注意到式（5.61）中前两式事实上比后两式要高一个量阶，即是高阶小量，可以略去，则

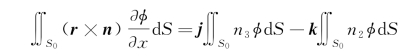
或者

式中，δ5i和δ6i为克罗内克尔δ符号。

应用式（5.60）和（5.62）的结果，式（5.59）可改写为

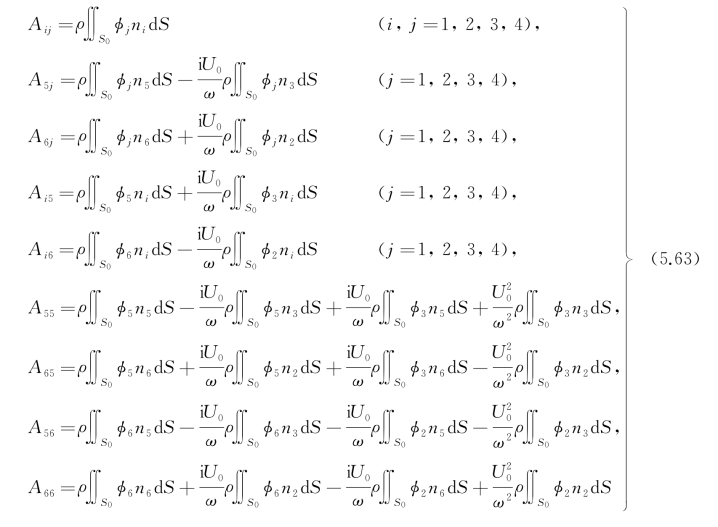
在上式的推导过程中，为了消除积分号内出现的，应用了船体细长的条件，这是目前摇荡辐射势定解问题得以成立的前提。

再者，在推导过程中，我们不曾对φj的量级作限制。原来，曾对辐射势Φ（x，y，z，t）作过假定，即它与运动量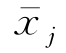同阶，是个一阶小量。经式（5.53）的分解，各运动模态相应的规范化速度势φj原则上应该是零阶量，物面条件为但是，在简化自由面条件时，引进了细长体假定，这反过来又对n j作了限制，比如n 1和n 4=yn 3-zn 2要比其他n j（j≠1，4）小，从而各φj的量级也不尽一致，如φ1和φ4就要比其余φj高一个量级。但在上面的讨论中，似乎都不必去顾及，这是其不一致（inconsistent）之处，即问题中所含各物理量的量级不完全一样。

从形式上看，式（5.63）中含有两种项：一是显含速度U 0，二是不显含有U 0。但这绝不意味着后一种项与速度U 0无关，因为其中辐射势φj是通过自由面条件［F］与速度U 0发生关系。后面第8章将会论述，若引入切片理论，这些项变得实际上与U 0无关，从而航速影响仅体现在显含速度U 0的项中（当然速度U 0还通过遭遇频率表现出来）。