船舶运动理论――三维脉动点源速度势

由上一节的讨论已经知道，只要选择合适的格林函数G（P，Q）≡G（x，y，z；ξ，η，ζ），使之满足一定的条件，则场内的速度势就可由此格林函数在物面S 0上的分布来确定，分布的强度则取决于物面边界条件。当水深无限时，格林函数应满足下列定解条件：

式中，k=ω2／g为波数。

显然，以上定解条件中第一式控制方程为泊松方程（Poisson equation），它表明在场内P=Q处格林函数有奇性，除此点外，G在场内是处处调和的。如暂且不考虑其他一些定解条件，则这一泊松方程的一个特解是源函数（不计常数的差别）

式中，P（x，y，z）为场点坐标，Q（ξ，η，ζ）为源点坐标，r（P，Q）=［（x-ξ）2+（y-η）2+（z-ζ）2］1／2为场点P至源点Q的距离。此函数表示Q点上强度为4π的点源（广义上不区分源和汇的差别）在P点引起的速度势。然而，需要的格林函数不仅要满足泊松方程，还应满足式（5.15）中的其他三个边界条件；显然，源函数式（5.16）不能满足这一要求。但正如前文所指出，式（5.16）只是泊松方程的一个特解，因此，它的形式不是唯一的。事实上，在源函数式（5.16）上加上任一在整个流场内处处调和的函数G*（P，Q），即

都能满足泊松方程，附加项G*（P，Q）的引进使格林函数G具有很大的灵活性，G*（P，Q）的合适选取有可能使整个定解问题式（5.15）得到满足。

进一步考察定解问题式（5.15），特别是其中的自由面条件［F］，容易看出，格林函数式（5.17）的强度必须是简谐脉动的，圆频率为ω，否则自由面条件不能写成当前的形式（这一点若与5.1节的叙述类比可看得更加清楚）。于是，设定强度以频率ω脉动的格林函数（以后简称作三维脉动源）在场内诱导的速度势具有形式

它定义在z≤0，且除去点Q（ξ，η，ζ）的流场内，G由式（5.17）定义。事实上，不管什么物理条件，速度势Φ应满足定解问题式（5.1），G应满足的定解条件式（5.15）。

式（5.18）表明，源的强度是周期性脉动的，当这个源置于水中相当长时间后，起始运动产生的瞬态（transient）扰动影响消失之后，整个流场的运动也就是周期性的了，其频率与源强脉动的频率相同。正因如此，才可以将势函数的时间变量与空间变量分离从而成为式（5.18）的形式。式（5.18）中G一般是复函数，即

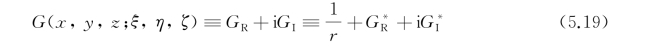
下标R和I分别表示复变量的实部和虚部。展开式（5.19），速度势Φ可写作

这意味着，式（5.18）的形式中已经隐含了源强作余弦脉动的假定。既然知道源强是余弦脉动的，是否可在式（5.20）中令G I=G*I≡0，即

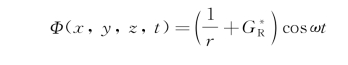
那样的G是实函数，也要求满足式（5.15）中所有的方程和条件。事实证明，这一做法是不可行的。如5.1节中的讨论，当有自由面存在时，流体运动不能与扰动同步脉动，流场各点处流体运动与扰动源的脉动间存在相位差，G*I（G I）就起有相位调节的作用；另一方面，无论是G R或G I都不能单独满足辐射条件，只有两者的组合才有可能。事实上，辐射条件决定解的唯一性。

在决定源函数G（即求G*）时，从自由面条件入手。将式（5.17）代入定解问题式（5.15）中的自由面条件，在z=0时得到

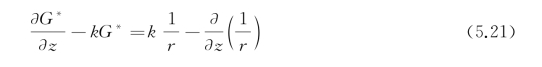
应用的傅里叶（Fourier）重积分表达式（参见本章附录）：

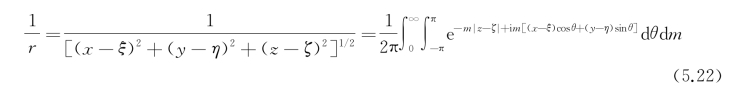
在式（5.21）中，需要的是或其导数在z=0上的值。由于ζ＜0，有z-ζ＞0，故上式中，-m|z-ζ|=-m（z-ζ），于是

式（5.21）的右端变为

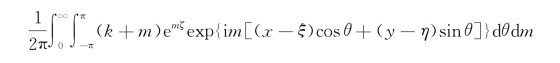
对比两端，不妨令G*（x，y，z；ξ，η，ζ）具有如下形式：

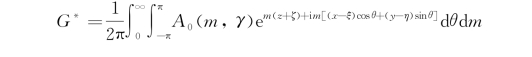
其中被积函数与一样保证了G*满足拉普拉斯方程，即G*是调和的，因子e m（z+ζ）使z→-∞的无限深处条件能够被满足。与不同的是，在G*整个z≤0的下半空间内是调和的，指数-m|z-ζ|已被m（z+ζ）所代替，这相当于奇点可在上半空间存在。将其代入自由面条件式（5.21）两边，经比较可知：

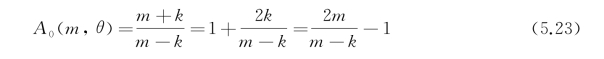
于是，在形式上得到

式中，r 1=［（x-ξ）2+（y-η）2+（z+ζ）2］1／2；上式中第二和第三个等式引用了的傅里叶重积分表达式。

这样得到的点源函数G（x，y，z；ξ，η，ζ）在形式上满足了式（5.15）中除辐射条件外的全部定解条件。但在式（5.24）中，被积函数在m=k处有一奇点，这个积分若不重新解释就是无意义的（在黎曼积分意义上）；然而，不同的解释其结果又不同，只有其中能满足辐射条件的解释才是需要的。

沿实轴（0，∞）积分时，在m=k上有奇点，如图5.1所示，该积分可做三种解释：一是取积分路径L 1，从m=k上面绕过；二是取积分路径L 2，它不经过奇点m=k，而取积分的柯西（Cauchy）积分主值；三是取积分路径L 3，从下面绕过奇点m=k。积分路径的最后确定须根据这些积分在无穷远处的渐近表达能否满足辐射条件。为讨论按不同的积分路径所得积分在无穷远处的渐近性质，引入

式中，R=［（x-ξ）2+（y-η）2］1／2。这时，式（5.24）可改写为

图5.1　积分路径的定义

式中，

式（5.25）中第2个等式来源于cosθ是周期函数；第3个等式应用了贝塞尔函数（Bessel）函数的一个积分表达式：

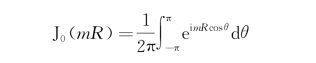
式（5.25）中第4个等式来源于绕奇点m=k的半个留数，P.V.是积分取柯西主值的意思。

在远离源点处的量级，而

注意到

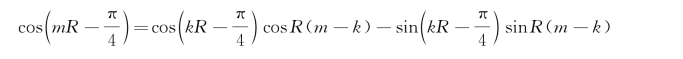
再应用傅里叶积分的一个定理［124］：若函数f（x）在［a，∞）中是可微函数，x 0＞a时f″（x 0）存在；且f（x）／x和f′（x）／x在［a，∞）上是绝对可积的，那么，在R→∞时有

这个定理在波浪问题中也经常遇到的［132］。应用这些关系，根据式（5.25）即可知对应三种积分路径分别有渐近式：

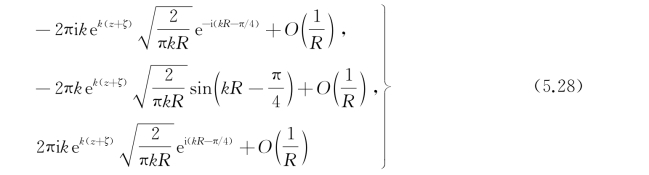
可以看出，由于G是与振荡因子e-iωt相配的，因此，沿路径L 1的解在远方（R→∞）的渐近式中含因子e-i（kR+ωt-π／4），它表示一个向内传播的波浪，与辐射条件的要求相反；沿路径L 2，势函数在远方的渐近式含因子，这是一种驻波，波既不内传也不外传，与辐射条件的要求不符；只有沿路径L 3的积分所给出的势函数在远方的渐近式中含因子ei（kR-ωt-π／4），是一个外传波，符合辐射条件的要求。于是，所要求的点源表达式为

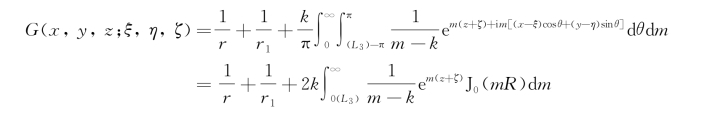
它在R→∞处有渐近式

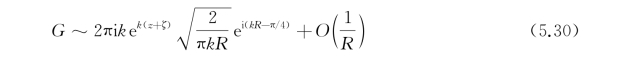
这些结果告诉我们：(www.xing528.com)

（1）三维脉动源的势函数在远方的渐近式是一个外传的正弦波，其波幅按的速率衰减。容易验证，式（5.30）符合定解条件式（5.15）中辐射条件的数学表达式。

（2）G I（x，y，z；ζ，η，ζ）=2πk e k（z+ζ）J0（kR）不仅体现了场内各点上流体运动的相位与源强度变化的相位有差别，而且与G R结合在一起满足了辐射条件，保证了解的唯一性。

当水深有限，深度为H，则定解问题（5.15）中底部条件应改为；自由面条件［F］中ω2／g不再能记作k，因为这时波数k不等于ω2／g，它们之间存在色散关系，若仍以ν记ω2／g则

现选取三维脉动源的形式为

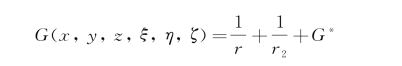
式中，r 2=［（x-ξ）2+（y-η）2+（z+2H+ζ）2］1／2，可见是在池底以下，相对于池底与点（ξ，η，ζ）对称的点上的一个映象源，它在流体域内与G*一样是处处调和的。与前文类似，可得

式中，ν=ω2／g，它与波数k满足色散关系（5.31）。

上式右端第3项的被积函数中也有一个奇点m=k，k是分母m sinh m H-νcosh m H=0的根。式中最后一项是积分路径从下面绕过奇点（即前述路径L 3）时所得的半个留数，而

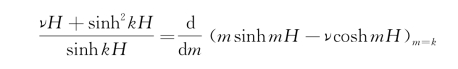
是在求留数时出现的。即

式中，R 2=（x-ξ）2+（y-η）2和　

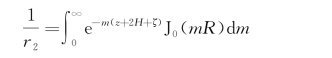
可得

现设G*具有如下形式：

其中被积函数的选取保证了G*既满足拉普拉斯方程，又满足池底条件。容易证明

于是

应用留数定理，即可得式（5.32），该式在无穷远处的渐近式满足辐射条件。

式（5.32）还可写成级数形式［124］，即

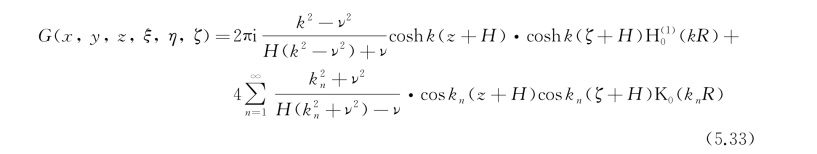
式中，k n为方程k ntan k nH+ν=0的正实根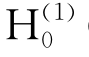，（kR）为第一类的零阶汉开尔（Hankel）函数，K 0（k nR）为第二类零阶修正的贝塞尔（Bessel）函数，其他变量的定义与前文相同。

事实上，与振荡因子e-iωt相配，含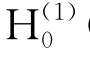（kR）的项在无穷远处表示向外传播的辐射波，K 0（k nR）诸项在远方以e的负指数型快速衰减，故前者代表波动项，后者则表示局部扰动项。

任一有限尺度的物体在自由面上作简谐摇荡时，在远离物体处，这一振荡运动的影响即可看作是脉动点源或其某种分布的影响。当然这时远方辐射势和辐射波在周向一般是不均匀的。若用柱坐标（R，θ，z）描述，则出现对极角θ的相关。下面将简要地讨论物体在自由面上做简谐摇荡时远方辐射波的表达形式。

在kR≫1的远方，式（5.33）中的局部扰动项已经消失，只有波动项体现出来，就是

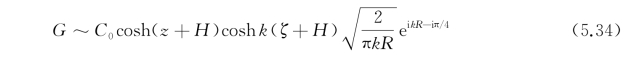
这里（kR）已经写成它在kR→∞时的渐近形式，C 0是个常系数，取为

采用柱坐标，记

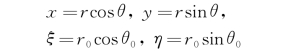
这里r、r 0分别为场点P和源点Q至柱坐标垂向轴的水平距离；θ、θ0即为r和r 0的辐角或极角。当讨论R→∞时速度势的渐近形式时，实际上是讨论r 0保持固定的有限值，r→∞的情况。

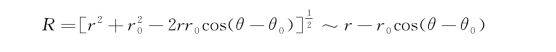
于是，式（5.34）为

将上式代入速度势的表达式（5.12），并略去下标j以简化书写，即可得φ在无穷远处的渐近式为

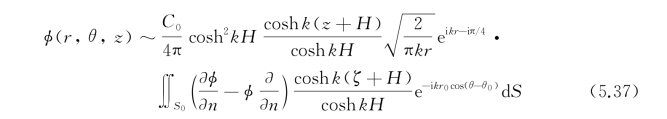
当水深k H→∞时，取上式的极限得

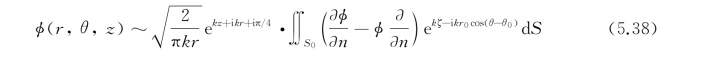
上面两式中的积分常定义作科钦函数（Kochin's function）H（θ），有限深水为

无限水深为

式中，积分在物面S 0上进行，变量为（ξ，η，ζ），也可将变量记作（x，y，z），则更符合习惯表示法。于是，式（5.37）可记作

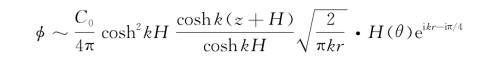
它也可写成

把Λ（θ）定义为远场波幅，这是因为远场波形

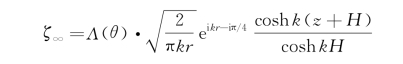
Λ（θ）与科钦函数H（θ）的关系：

水深趋于无穷时，式（5.43）可写成

上述科钦函数的定义和势的远场表达对每一运动模态都是适用的。既然场内总辐射势可表示成各运动模态规范化速度势的线性叠加，容易看到科钦函数的定义和辐射势的远场表达也同样适用于场内总的辐射势。顺便指出，这些表达也同样适用于场内的绕射势及绕射势与辐射势的线性叠加，因此，在绕射问题中不再讨论。