无航速船舶产生速度势的简谐振荡

简单起见，先不妨以船舶无航速在静水自由面上作摇荡运动为例，按第4章所述，船体摇荡时流场中一阶不定常速度势Φ（x，y，z，t）的定解问题为：

式中，U j及n j分别为物面运动的广义速度和物面上某点的广义法向矢量，下标j指上述矢量相应于第j个运动模态的分量，它们都在第4章中作过定义。另外，为简洁起见，将辐射势ΦR简写作Φ，略去下标R，这样做在这里不致引起混乱。

上述定解问题的表述对任意形式的船舶摇荡运动都是适用的。然而，这一表达对我们目前所要讨论的主题来说显得过于广泛。当我们研究船舶在规则波中的摇荡运动时，精确到一阶量，船舶运动的整个动力系统即可认为是一个线性系统，它的输入是规则波的扰动，是个简谐的振荡输入，显然，系统的输出（船舶的受力、运动等）也必然是个简谐振荡量，当然两者的振荡相位可能有差异。即使入射波是不规则的，只要线性假定依然成立，不规则波可以分解成无穷多个单向单频的规则波的叠加，我们仍然可以将问题转化成船舶对规则波扰动的响应来进行讨论。由此可见，船舶的简谐振荡运动是船舶摇荡运动的一种基本的运动形式。作为相应的辐射问题，本节将讨论船舶在静水自由面上作简谐的强迫摇荡运动时所产生的速度势。

现设船体在平衡位置周围作微幅的简谐摇荡运动，其圆频率为ω，瞬时位移为

式中，Re｛　｝表示取括号内的量的实部；j表征运动模态，j=1，2，…，6；为某个运动模态的复数运动幅值，它不仅表述了运动的真实幅值，还反映了运动的相位。事实上，若令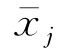=，其中下标R和I分别表示该物理量的实部和虚部，则式（5.2）又可记为

或者

这里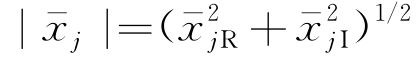，为第j个模态的运动幅值；α=tan-1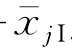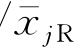（-／）为该模态的运动相位。当然，在船体作强迫振荡时，相位可以事先规定，如令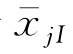=0。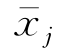取复数则代表更一般的情况，可以反映出不同运动模态间的相位差异；而且，这样规定可以与以后船体在波浪上运动的讨论统一起来，那时ξj的幅值和相位事先未知。

船体的摇荡运动速度U j≡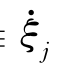，于是按式（5.2），有

这里“·”表示该变量对时间的一阶导数。

相应地，船体摇荡的速度势Φ（x，y，z，t）可设为

式中，φ（x，y，z）一般也是复数，因时间因子已分离出来，故φ中不再含有时间变量，它只与空间位置有关，所以也常叫作空间速度势（spatial velocity potentia1）。显而易见，空间速度势φ（x，y，z）的求解将是个定常问题。

一般而言，速度势的相位与扰动（现为船舶的摇荡运动）的相位是不同的。这是因为当有自由面存在时，外界扰动将在自由面上产生波浪，波浪传播需要时间，当扰动的强度以某一简谐形式脉动时，扰动的影响不能在瞬息间传遍整个流场，于是形成了场内各处流体运动与扰动之间的相位差。这是物体在有自由面的流场中运动和在不具有自由面的无限流场中运动时流体动力影响间的本质差别之一。当物体在不可压缩流体的无限流场中运动时，局部扰动将瞬息间传遍流场，这时，流体运动与扰动是同步的。(www.xing528.com)

另外，当把速度势设成式（5.4）时，实际上已经隐含地认为运动已经持续了一个相当长的时间，由船体摇荡初始动作引起的瞬态影响已消失，场内的流体运动已达稳态。将式（5.3）和（5.4）代入定解问题（5.1），可得空间速度势φ（x，y，z）要满足的定解条件为

式中，对于φ来讲，现在辐射条件可以写成显式，如式（5.5）中第5式所示。该式事实上是个一阶偏微分方程，它的一个通解是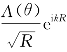，与振荡因子e-iωt相配，代表一个波幅以速率衰减的远方外传波。辐射波的波幅为Λ（θ），一般为极角θ的函数，即在水平的周向波幅可能有变化；辐射波的波数为k，当水深无限时，k=ν=ω2／g；若水深有限，深为H时，k与ν之间要满足色散关系：

上述辐射条件实际上表达了扰动波的能量辐射关系。

根据定解问题式（5.5）的线性性质和物面条件［S］右端的表现形式，可将势函数φ进一步分解。现取

式中，φj是与某一运动模态j相联系的速度势，它满足定解条件式（5.5），只是其中物面边界条件要修改为

容易看出，φj只与物体形状和运动模态j有关，与运动的大小无关。对给定的物体，在某一确定的振荡频率下，可一劳永逸地解出φj。事实上，φj也可看成是物体在j方向以单位速度摇荡时产生的速度势，称为规范化速度势（normalized velocity potential）。近来，也有一些文献将φ记成这时，式（5.8）变成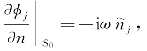相应地，φj可视为物体在j方向以单位振幅摇荡时产生的速度势。本书中选取前一种分解方式［见式（5.7）］。

现在回过来考察势函数分解式（5.7）的含义。根据式（5.4），场内速度势为

式中，下标R和I分别表示复数的实部和虚部。式（5.9）的右端第一项与无限流场中物体运动的势函数分解一样，与速度ξ·j成正比［131］；第二项则是物体在有自由面的流场中摇荡时所特有的，它与位移ωξj成比例。由于是简谐运动，与ωξj成比例又可理解为与运动加速度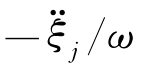成比例。这一项的出现体现了流体运动在相位上与物体运动的差别。此外，注意到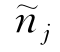总是实数，由式（5.8）易知，对φjR和φjI来说，有物面条件：

显然，φj R是物体运动的产物，而φj I则是物体静止时的结果。如果不管辐射条件，那么，只有平凡解，即φjI≡0。但事实上，速度势φ的辐射条件又可写成：

和

这里应注意作为变量的R和作为下标的R的区别。上面两式是紧密耦合的；在物理上两者共同组成了描述远方有向外辐射的前进波的边界条件，缺一不可。因此，φj I不应恒等于零。在φ中虚部φj I的出现不仅起到了调节相位的作用，还使得辐射条件能得以满足。