船舶运动理论：线性速度势分解效果

讨论了自由面条件和物面条件的摄动展开之后，可以将一阶速度势的定解问题作一些归纳。一阶速度势就是通常所谓的线性速度势。

由以上的讨论已知，无航速时的自由面条件和物面条件是有航速时相应条件在航速U 0取零时的特例，所以在这里从有航速的一般情况出发来建立一阶速度势的定解问题。而且，既然一阶势的物面条件已经变换成在物面的平均位置上满足，就没有必要再区分动坐标系变量和参考坐标系变量，故以下将坐标变量简单地记以x、y、z或x i（i=1、2、3）。

（1）在船体摇荡是小量的前提下，不定常一阶速度势Φ（x，y，z，t）的定解问题：

这里的扰动波是指由于物体存在振荡运动对入射波产生扰动而形成的波系，不包括入射波本身。上式中出现的变量都已在前几节中说明或定义过，这里不再重复。为叙述简洁，我们从现在起用［L］表示拉普拉斯方程，［F］、［S］、［B］分别指自由面条件、物面条件和底部条件，在底部条件［B］中，前一式适用于有限水深情况，后一式则适用于无限水深情况，［R］表示辐射条件。另外，船体定常移动的兴波速度势（x，y，z）的定解问题：

对这样的定解问题提法，要先解一个非线性的定常兴波问题，从中解出兴波势φ-（x，y，z）、自由面方程z=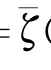（x，y）及船体相对于静止状态湿面积S 0的变化，亦即定常兴波情况下的湿表面、物面、波面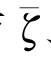、底面以及无穷远处的控制面构成了流体域的完整的边界，在这个域内求解一阶不定常势Φ（x，y，z，t）。

纽曼曾直接从这一对定解问题出发，应用匹配渐近展开法，针对细长体建立了一个“统一理论”（unified theory）［127，128］，简化了自由面条件，保留了物面条件中部分的影响。1980年由史克拉伐诺斯（Sclavanous）对其做了计算［129］，发现有航速时的计算结果要比通常的切片理论更好些（关于切片理论［16］，我们将在第8章中加以讨论）。

流场中任一点的压力p可分成两部分，即p=p 1+p 2，其中：

前一等式是船体定常兴波问题中的压力分布p 1Δ的关Δ系式，后一式则可确定不定常势Φ引起的压力分布p 2，其中包含了定常兴波的干扰，即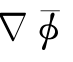·项。毋庸赘言，上式也是精确到ε一阶的量级。

众所周知，非线性定常兴波问题是一个至今尚未能完善处理的难题，为绕过这一困难，我们进一步引进定常兴波也是小量的假定，于是有下述第二类定解问题。

（2）船体摇荡和定常兴波都是小量。这时，一阶不定常速度势Φ（x，y，z，t）的定解问题是：

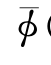定常兴波势（x，y，z）的定解问题变为（x，y，z）的定解问题在兴波阻力理论中称为诺依曼-开尔文（NeumannKelvin）问题［130］。流场中压力p仍可分成p=p 1+p 2，其中

在这一定解问题的提法中，定常兴波问题与不定常速度势求解问题是完全独立的，而且，流体域是事先已知的，因为自由面条件和物面条件都已经变换到在静水面z=0上和静水中船体湿表面S 0上来满足。

从不定常势定解问题中容易看出，拉普拉斯方程和边界条件都是线性的，可应用叠加原理把速度势加以分解。令不定常势Φ（x，y，z，t）为

式中，ΦI（x，y，z，t）是入射波速度势。由于在建立线性定解问题时是以船体摇荡小为前提的，事实上这已经隐含假定了入射波也是小量，即所谓的微幅波假定，因此，这里ΦI与ΦD和ΦR一样，亦应是一阶量。ΦD称为绕射势，ΦR称为辐射势，它们的含义将在后面阐述。流场中总的速度势应是定常兴波势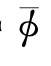与不定常势Φ之和，即(www.xing528.com)

将式（4.66）代入定解问题式（4.64），显然可见ΦI、ΦD和ΦR各自都应满足拉普拉斯方程［L］、自由面条件［F］和底部条件［B］，只要在形式上将这些表达式中Φ分别添注下标I、D、R即可。ΦD和ΦR还应满足无限远处有外传波的辐射条件。关于ΦI，在本书讨论的范围内，我们一般取其为单一频率、单一方向的平面入射波速度势，它作为已知的输入给出，无所谓辐射条件。剩下的是需要满足物面条件［S］。即

对此，可作如下的选择，即

这样，在线性理论范围内，不定常速度势Φ的定解问题可分解成速度势ΦD和ΦR的两个定解问题。这两个定解问题是互相独立的，而且，除了物面条件有所不同之外，其他一些边界条件和控制方程均相同。

将物面条件式（4.67）略加变形，有

由上式容易设想，物面运动的法向速度为零，即物体是固定不动的。入射波在这一固定的物面上诱导有法向速度，而ΦD的产生正是为了抵消这一法向速度，使得物面条件得到满足。由此可见，ΦD表示一个固定物体的存在对入射波流场的扰动，或者说表示固定物体存在引起的波浪绕射影响，因此，把ΦD称为绕射速度势（diffraction potential），相应的定解问题称为绕射问题。

类似地，由ΦR的定解条件可知，ΦR与入射波势ΦI及绕射势ΦD无关。从要满足的物面条件（4.68）看，ΦR仅与船体振荡运动时船体表面上各点的法向速度有关。这说明，当求解ΦR时，完全可以不计入射波及其绕射，而认为船体在有自由面的静水中作某种给定形式的摇荡运动。众所周知，一个有限尺度的物体在自由面上摇荡将产生波浪，波从物体向四周辐射出去，故而称作辐射势（radiation potential），相应的定解问题称为辐射问题。

波浪问题中线性速度势的这一分解最早由哈斯金特提出。由于此分解明显的优点和由此带来的一系列有意义的物理概念，使得这种分解成为迄今为止求解物体摇荡运动时线性速度势问题的经典处理方法。

值得指出的是，上述分解只有当定常运动兴波是小量时才能施行，若没有这一前提条件，分解就有困难。事实上，当定常兴波不是小量时，流场中的不定常势Φ要满足的自由面条件是式（4.62），且这一条件须在定常兴波波面上得到满足。简单些讨论，设ΦR≡0，即设物体没有摇荡运动，只在有入射波的流场中作定常移动，这时Φ=ΦD+ΦI，若将其代入式（4.62），尽管从形式上看，该式对Φ（ΦD和ΦI）是线性的，但也不能把ΦD和ΦI分开。因为给定的ΦI满足的自由面条件不是式（4.62），且满足条件的位置也不在定常兴波波面上，容易证实，在移动参考系o′x′y′z′中，ΦI应在z′=0的静水面上满足式（4.64）中的自由面条件。这样，由式（4.62）仅能得到一阶绕射势ΦD在定常兴波面上满足的自由面条件，它不是齐次的，在右端项中将出现与ΦI有关的项。

定常兴波为小量的极限情况即是无航速的情况，这时船速U 0≡0，自由面条件即变成简单的形式：

它对ΦI、ΦD和ΦR均适用；辐射势ΦR的物面条件也简化成

由于没有航速，就无所谓定常运动的耦合影响，得出上面两式是显然的。

关于辐射势和绕射势定解问题的求解及有关物理概念的引进和讨论，将在之后的章节中进一步深入地展开。