船舶波浪上运动理论成果

在自由面条件的摄动展开中，我们利用了自由面上的扰动是小量这一前提；展开后，各阶次速度势均满足线性的自由面条件，而且满足条件的自由面位置一律近似到z 0=0的静水面上，即自由面运动的平均位置。原先的自由运动边界变成了固定边界。

另外，物面也是流场的一个运动边界。物体作摇荡运动时，应该在物体的瞬时位置上满足物面的不可渗透条件，但在小振幅运动的假定下，瞬时位置与平均位置的差别是小量。为与处理自由面条件的做法一致，对物面条件也要作摄动处理。把要求在物面瞬时位置上满足的条件化成在平均位置上满足物面条件，从而将物面运动边界变换成固定边界。

为了使问题的叙述更为清晰，我们从没有航速的情况入手。

如图4.4所示，o 0x 0y 0z 0为空间固定坐标系。因为没有航速，它也是参考坐标系o′x′y′z′（详见4.1节中定义）。为方便后面易于推广到有航速情况，这里直接采用参考坐标系o′x′y′z′。

图中S 0是船体的平均位置。船体运动时，有一动坐标系oxyz与之固结。显然，当船体没有摇荡时，坐标系oxyz与o′x′y′z′重合。摇荡时，动坐标系原点o在参考系中的坐标为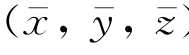），它表征着船体的线位移运动，即纵荡、横荡和垂荡。此外，船体还绕o点的瞬时轴转动，其姿态由欧拉角α、β、γ规定。

静止时物面S 0上的某一点P 0，其坐标记以（x′0，y′0，z′0），该点上的单位法线矢量为n P0，与以前一样，可取n P0为物体的内法线（对流体域而言是外法线）。物体运动时，在某一瞬时由P 0点的位置移到了P点。在参考坐标系（无航速时就是空间固定坐标系）中，P点的坐标是P=（x′，y′，z′）；在动坐标系中P=（x，y，z）。因无摇荡时，动坐标系与参考坐标系o′x′y′z′重合，故显然有P=（x，y，z）=（x′0，y′0，z′0）。P点在参考坐标系与动坐标系中的坐标变量的关系为

矢量o′P在参考坐标系o′x′y′z′中的分量是（x′，y′，z′）；o′o的分量是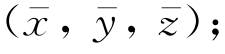；在以o点为原点并与参考坐标系o′x′y′z′三轴平行的另一参考坐标系中，矢量oP可记为：oP=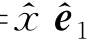++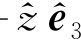3，其中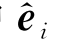（i=1，2，3）为参考坐标系三个坐标轴的单位矢量；在动坐标系中oP又可表达为oP=x e 1+y e 2+z e 3，其中e i（i=1，2，3）为动坐标系三个坐标轴的单位矢量。根据4.2节叙述内容：

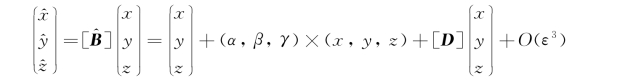
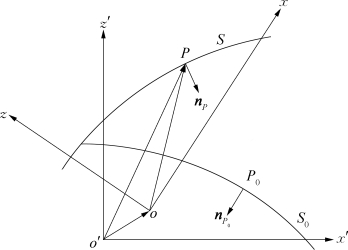
图4.4　平均物面与瞬时湿表面

式中，

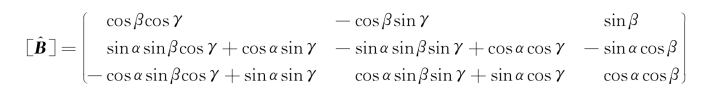
这里定义

它是二阶小量，且

于是

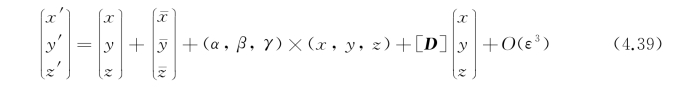
根据微幅运动假定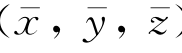，（）和（α，β，γ）是一阶小量，（α，β，γ）×（x，y，z）又可记为εijkαjx k，其中令｛αj｝=（α，β，γ），｛x k｝=（x，y，z）（j、k=1，2，3）。［D］中包含的是α，β，γ的平方项或互乘项，因此是二阶小量。上式中（x，y，z）=（x′0，y′0，z′0）不是小量，而是船体表面S上某点P相对于动坐标系的坐标分量，也是物体在平均位置时，S 0上相应的点P 0在参考坐标系o′x′y′z′中的坐标分量。

定义在参考坐标系o′x′y′z′中的势函数φ（x′，t）在船体表面瞬时位置上的数值是

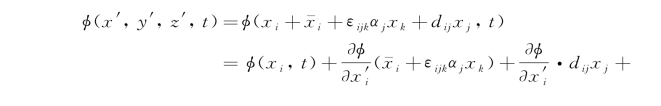
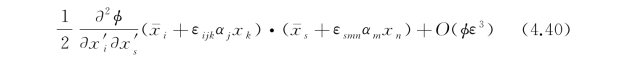
为书写简便已令x i=（x 1，x 2，x 3）=（x，y，z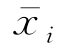），和x′i仿此；αj=（α1，α2，α3）=（α，β，γ）；d ij为矩阵［D］的相应元素。

上式中右端第一项φ（x i，t）=φ（x，y，z，t）=φ（x′0，y′0，z′0，t）表示φ在静止物面S 0（即　平均位置时物面）上的值，第二项是φ的导数与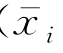（+εijkαjx k）的乘积，导数是对参考系坐标变量｛x′i｝=（x′，y′，z′）的导数，其值取在静止物面S 0上。由于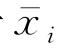=O（ε），αj=O（ε）（i，j=1，2，3），所以该项的量级是O（φε）。其余两项的意义类似，量级分别为O（φε2），O（φε3）。

在物面条件中出现的是瞬时物面S上φ的法向导数值，即

式中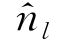，（P）为瞬时物面上P点的单位法线矢量n P在参考系坐标轴上的投影。仿照式（4.40），导数可表达为

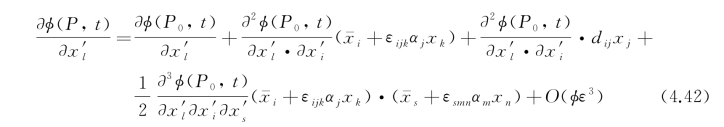
式（4.41）中P点的法线矢量n P在参考系坐标轴上的分量（P）也要设法用P 0点的量表示，因为对于微幅运动，此分量的变化中也含有小参数ε。

单位法线矢量n P与n P0分别可表示为

这里n q是相同的。另一方面，n P又可以在参考坐标系中表达为

式中，是参考系坐标轴上的单位矢量；e q是动坐标轴的单位矢量。根据4.2节的推导可知

故有

或者

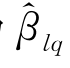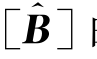因为就是矩阵的元素。

于是由式（4.41）可得

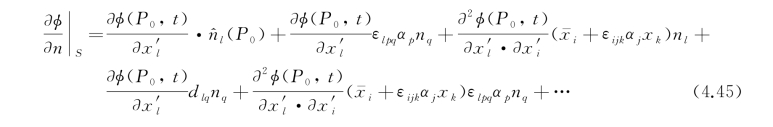
上式右端第一项是P 0点上的，第二项是动坐标系旋转所致，第三项是速度梯度引起的，之后是二阶及二阶以上的小量。

现在考虑物体表面S上P点的运动速度U（P）。船体无航速摇荡时：

式中，r=oP，ω在动坐标轴上的分量为

于是

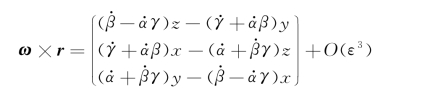
其也是在动坐标系中表达的。

速度U（P）的法向投影为U（P）·n=U n，它可记为

物面条件要求式（4.45）与式（4.46）相等，注意到φ=εφ（1）+ε2φ（2）+…，易得到

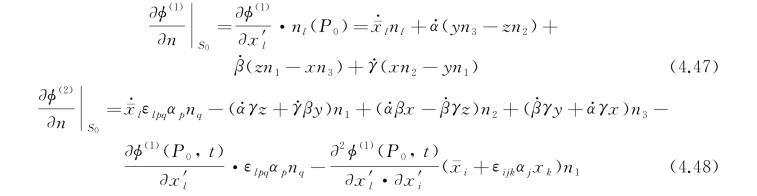
上面两式中给出了一阶速度势φ（1）（x′，t）和二阶速度势φ（2）（x′，t）分别需要满足的物面条件，现在物面条件是在船体的平均位置S 0上得以满足的。

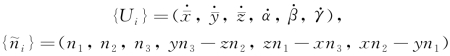
引入广义速率和广义法向矢量的符号：此处n i、x i为物面平均位置S 0上法线矢量和位置坐标在参考系坐标轴上的投影。于是一阶度势φ（1）（x′，t）的物面条件可记为

这个形式与物体在无限介质中运动的情况类似。

当船体有航速时，仍以参考坐标系o′x′y′z′来表达。根据4.1节中的定义，参考系o′x′轴与空间固定坐标系o 0x 0y 0z 0的o 0x 0轴重合，船舶以航速U 0沿o 0x 0轴移动。这时，在参考系中速度势记为（x′，y′，z′，t）。物面条件的精确提法是在物体任一瞬时表面S上：

式中，n是物面S上的单位法线矢量，像往常一样，以指向流体外域为正。U是船体湿表面上的当地速度，即

(www.xing528.com)

式中，是参考坐标系中的单位坐标矢量；ω是物体旋转角速度，r是物面上某点到动坐标系原点o的位置矢量；动坐标系固结在物体上，无摇荡时o点与o′点重合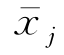，（t）是o点在参考系中的坐标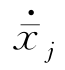，（t）是相应的速度分量。

如4.3节所述，船体边移动边振荡时，其速度势可分成是定常移动的兴波速度势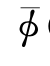（x′，y′，z′）与不定常速度势Φ（x′，y′，z′，t）之和，即

将上式及式（4.50）代入式（4.49）得到不定常速度势Φ（x′，y′，z′，t）的物面条件为

式中，n指瞬时物面S上的单位法线矢量。

若物体没有摇荡运动，则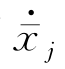=0，ω=0，这时，物体表面在参考坐标系内是静止的，将以湿表面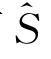表示之。注意湿表面与S 0是不同的，S 0是处于平均位置的船体在静水中的湿表面，而则在S 0上叠加了由于定常移动兴波引起的湿表面变化。物面条件：

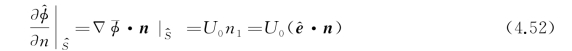
这是物体移动兴波的定常物面条件，它与自由面条件（4.29）是对应的。在形式上，它与式（4.51）中右端第一项等价，只是后者是在S而不是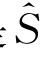上满足的，故不能消去。现在引入第一个假定，即不定常运动是微幅振荡，从而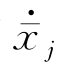、ω和Φ（x′，y′，z′，t）都是小量，记以O（ε）；相应地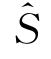，和S的差别也是同级小量。任意函数A（x′，y′，z′）在S上的值可在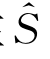的邻域作泰勒展开，从而可用函数A在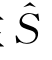上的值及其任意导数表示其在S上的值。按式（4.39）有

于是A（x′，y′，z′）可展开成

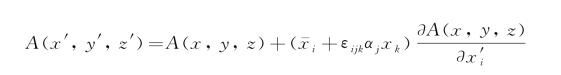
式中，A（x′，y′，z′）是函数A在S面上的值，A（x，y，z）和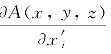分别是A在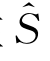面上的函数值和导数，因为在动坐标系中物面S上任一点的坐标（x，y，z）就是物面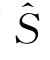上该点在参考系o′x′y′z′中的坐标。

取，则

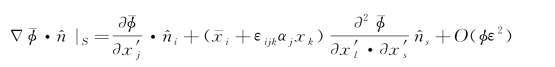
考虑到式（4.44），上式还可进而写为

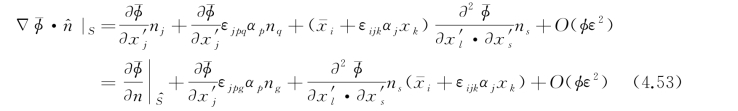
式中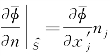，，由式（4.52）知，它应该等于U 0n 1。另外，式（4.51）的第一项中，U 0·n=U 0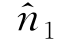=U 0［n 1+（α2n 3-α3n 2）］，其中（α1，α2，α3）=（α，β，γ），于是

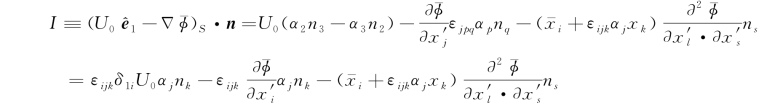
令

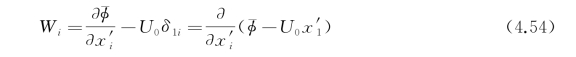
则

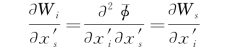
I又可写成

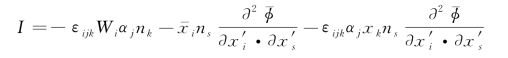
应用下述简单性质：

可得

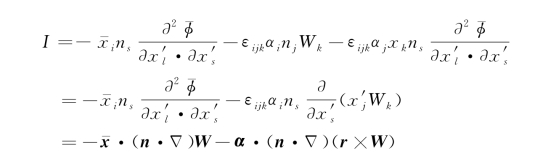
上式最后一行是I的矢量形式。将上式代入式（4.51），得到物面条件的新形式：

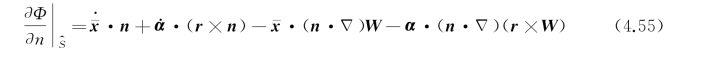
设广义位移定义为

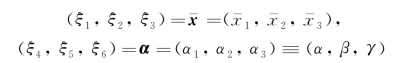
并定义

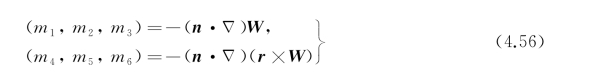
则物面条件（4.55）又可写成

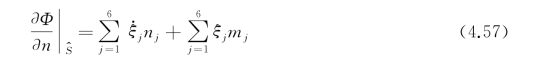
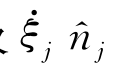原来在瞬时物面S上满足的条件现在需改为在计入定常移动兴波的平均物面上满足。实际推导过程中，还应用了之差及与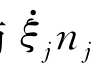之差都是二阶小量的事实。因为式（4.57）中各项都是一阶的量级，认为式（4.57）在S上满足条件。式（4.57）中右端第二项ξjm j表征微幅运动ξj与定常兴波m j的干扰。这一项曾长期被人忽略，包括像海夫洛克那样著名的学者［125］。在船舶流体力学中首先唤起人们注意此干扰项的是梯曼和纽曼（Timman，Newman）［126］。

如果进一步引入第二个假定，即船体移动的定常兴波较小，，式（4.54）给出

由定义式（4.56）有

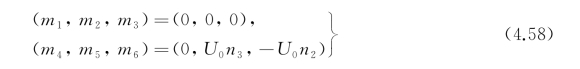
这时边界条件又可看作是在静止时的湿表面S 0上满足的，因为S 0与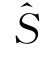也只差一阶小量。

对应S 0上的物面条件（4.57）和（4.58），不定常势要求满足的自由面条件是式（4.38）。而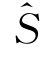上的物面条件（4.57）和（4.56）则对应于不定常势的自由面条件（4.36）。

在文献中还经常遇到利用其他形式表示的物面条件。如

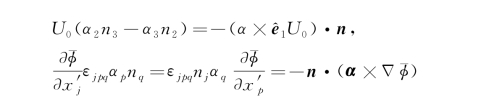
则I又可写为

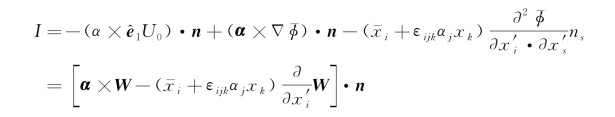
若引进符号

则物面条件（4.51）可改写成

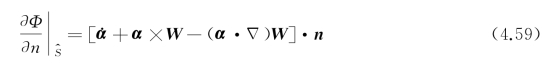
容易验证

所以

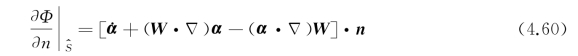
应用矢量关系A×（B×C）=（C·A）B-（A·B）C，上式又可写为

上述物面条件形式由梯曼和纽曼于1962年首先得到的。

如果定常兴波小，则上式可化为

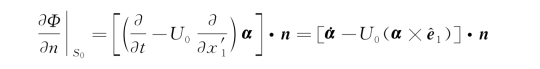
其中应用了

由上述推导可知，经摄动处理，原先须在瞬时物面上满足的边界条件现变换成在物面平均位置上满足的边界条件，边界位置是固定的，这对问题的求解带来极大的方便。