在推导角速度与欧拉角关系之前,我们先来证明两个等式。
令动坐标系oxyz三个坐标轴上的单位矢量分别为e 1、e 2和e 3,参考坐标系 的三个坐标轴上的单位矢量分别记为
的三个坐标轴上的单位矢量分别记为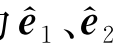 和
和 。显然,参考坐标系
。显然,参考坐标系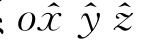 与参考坐标系o′x′y′z′相应的坐标轴始终是平行的,故坐标系o′x′y′z′上的单位矢量亦是
与参考坐标系o′x′y′z′相应的坐标轴始终是平行的,故坐标系o′x′y′z′上的单位矢量亦是 和
和 。这些坐标系都是正交的,因此任一矢量在不同的坐标系中可分别表示为
。这些坐标系都是正交的,因此任一矢量在不同的坐标系中可分别表示为
或者
式中,A j=A·e j是矢量A在动坐标系中的三个分量; 是矢量A在参考坐标系
是矢量A在参考坐标系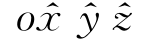 中的三个分量。
中的三个分量。
作为一个矢量e i,对任一固定的i,当然可以像矢量A那样用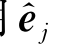 表示,即在式(4.14)中令A=e i,得
表示,即在式(4.14)中令A=e i,得
这里已定义
它表示动坐标系中i轴上的单位矢量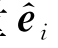 在参考坐标系中j轴上的投影。
在参考坐标系中j轴上的投影。
类似地,也可以把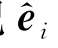 用动坐标系中的单位矢量e j来表示。在式(4.13)中令A=
用动坐标系中的单位矢量e j来表示。在式(4.13)中令A=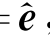 ,即
,即
这里定义
它表示参考坐标系中i轴上的单位矢量在动坐标系中j轴上的投影。
显然,比较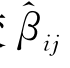 与βij的定义,易知:
与βij的定义,易知:
可将上式写成矩阵的形式。若记
按式(4.17),两个矩阵间有关系式:
这就是要建立的一个关系式。
另一方面,将式(4.15)和(4.16)写成矩阵形式,应有
和
由前一式可得
式中,[B]-1为矩阵[B]的逆。由后一式及式(4.19)得
比较上面两式立即可得
即
式中,[I]为一单位矩阵,即
式(4.20)是要推导的第二个等式。式(4.20)简单展开后可写成:
式中δik为克罗内克尔函数δ,即
上面两式表明,矩阵[B]的同行或同列元素乘积之和为1,不同行或不同列的元素乘积之和为零。显然式(4.20)对矩阵[ ]也是成立的,即(https://www.xing528.com)
]也是成立的,即(https://www.xing528.com)
现选择矢量A=r,r为某点到动坐标系ox yz原点o(因而也是参考坐标系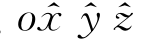 的原点)的矢径。在这两个坐标系中,该点的坐标分别为(x,y,z)和(
的原点)的矢径。在这两个坐标系中,该点的坐标分别为(x,y,z)和(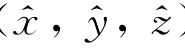 ),或记为(x 1,x 2,x 3)和
),或记为(x 1,x 2,x 3)和 )。由式(4.13)得
)。由式(4.13)得
于是有
或者
即
将上式与式(4.7)相对照,可见矩阵 ]就是式(4.7)中的转换矩阵,即
]就是式(4.7)中的转换矩阵,即
该式把两个坐标系中单位矢量的投影关系与欧拉角联系了起来。从中不难看出,矩阵[L],[M],[N]分别可看成是矩阵 的特例(若只围绕某一根轴旋转的话),因此,[L],[M],[N]也都满足关系式(4.21)。
的特例(若只围绕某一根轴旋转的话),因此,[L],[M],[N]也都满足关系式(4.21)。
记住了上述关系,下面即可建立角速度与欧拉角的关系。
设船体转动的角速度为ω,它在动坐标系中可表达为
在动坐标系中,某一轴上的单位矢量e i不随时间而变。当动坐标系转动时,e i的矢端速度为
或者
这里定义
另一方面,按式(4.15)可把e i写作![]() 是参考坐标系中坐标轴上的单位矢量,它既不转动,又不随时间而变。显然应该有
是参考坐标系中坐标轴上的单位矢量,它既不转动,又不随时间而变。显然应该有
比较![]() 的两个表达式,可知
的两个表达式,可知
{γij}是由角速度在动坐标轴上的投影构成的矩阵,{βij}则可认为是由欧拉角关系式所组成,展开上式,将会得到角速度与欧拉角的关系。
将式(4.23)写成矩阵形式:
注意矩阵[L],[M],[N]都满足关系式:
则上式又可记为
式中,
综合以上各式,并对比两边,容易得到
这就是所求角速度在动坐标系中三个分量(ω1,ω2,ω3)与三个欧拉角的关系。在解船体运动方程过程中得到ω=(ω1,ω2,ω3)后,即可由上式解出α、β、γ角。上式是一组联立的非线性常微分方程组,在给定初始值条件下可用数值方法求解。
这样,对在波浪中运动的船体,其位置和姿态都可以完全确定了。
若限于微幅摇荡,α、β、γ及其时间导数都是小量,准确到一阶量时,式(4.24)可近似地写成
也就是说,微幅振荡时,船体转动角速度在动坐标轴上的投影就可近似地认为是三个欧拉角的角速度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




