坐标系选取与运动量描述

在研究船舶在波浪上的运动时，常采用三个坐标系统。坐标系o 0x 0y 0z 0固定在流场中，不随流体或船体运动。通常选择o 0x 0y 0平面与静水面重合，o 0z 0轴铅直向上。用这个空间固定坐标系来描述入射波最为方便。第二个坐标系oxyz与船体固结，随船体一起摇荡，即所谓的动坐标系。在这个坐标系中表述船体表面时，船体表面方程将不含时间变量。一般的船舶是对称于中纵平面的，我们取ox轴的船舶是对称于中纵平面，并指向船艏；当船舶处于平衡位置时，oxy平面与静水面重合，oz轴垂直向上，位于二分之一船长处。另一个坐标系为o′x′y′z′，当船舶处于平衡位置时，它与动坐标系oxyz重合，但它不像动坐标系随船摇荡，而是始终位于平衡位置上。若船舶有平均直线航速，则该坐标系亦随船一起以此平均前进速度移动，它构成了表征船舶摇荡位移和姿态的基准，称为参考坐标系。

现设参考坐标系o′x′y′z′以速度U 0移动，o′x′轴与U 0的指向相同，o′x′轴与固定坐标系o 0x 0的夹角为δ。显然平面o′x′y′始终与o 0x 0y 0平面重合，也在静水面上；o′z′轴与o 0z 0轴始终平行，均垂直向上（见图4.1）。

两个坐标系的坐标变量间的关系由下式给出：

图4.1　固定坐标系与移动坐标系

动坐标系oxyz在参考坐标系o′x′y′z′中的相对位置描述了船舶摇荡的运动姿态和量值。

设在参考坐标系中，动坐标系原点o的位置在点（），则它们将是运动时船体相对参考系的线位移。对振荡运动来说，习惯上把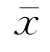称为纵荡，称为横荡，称为垂荡或升沉。如果o点正好与船的重心G重合，则坐标量确定了船体重心相对参考系的位置。它们和参考系原点的位移一起描述船舶重心在空间运动的轨迹。如果o点不与重心G重合，那么只有知道船体相对o点的旋转之后，才能确定重心的位移。

船舶摇荡运动时的姿态由动坐标系的转动来描述。若没有旋转时，动坐标系的位置在上（这时只有线位移振荡），转动后，动坐标系oxyz转到某一新的位置，则动坐标系相对于原先未转动时位置的角位移决定了船舶运动的姿态（见图4.2）。

角位移可用三个欧拉角来定义。假设动坐标系oxyz原来在位置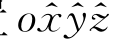上，经三次转动转到目前的位置，或者说坐标系经三次旋转，转到与动坐标系oxyz重合。

图4.2　坐标系的旋转　

图4.3　欧拉角

如图4.3所示，首先将坐标系绕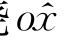轴转动一个角度α，使得轴转到由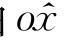轴及oz轴确定的平面上，得到一个新的坐标系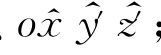；然后将这一新坐标系绕轴转动β角，使轴转到与oz轴重合，得坐标系，这时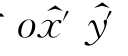坐标平面已与动坐标系的坐标平面ox y重合；接下来再将坐标系绕oz轴转动γ角，就可以与给定的动坐标系重合。这三个旋转角度完全决定了船体在空间的姿态。α、β、γ角称为欧拉角，分别定义了船舶横摇、纵摇和艏摇的角位移。

坐标系与ox yz中坐标变量的关系可通过简单的坐标变换得到。第一次坐标系旋转：

(www.xing528.com)

第二次旋转：

最后一次旋转：

式中，［L］、［M］、［N］分别代表以上三式中相应位置上的转换矩阵。综合以上三式，最终可得

在船舶摇荡问题中，多数处理的是偏离平衡位置较小的振荡运动，即船体的姿态角（角振荡位移）α、β、γ较小。在这个前提下，保留到一阶小量，有

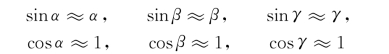
同理，在式（4.7）的变换矩阵中略去α、β、γ间的乘积项（它们是二阶小量），得

上式的逆为

若以向量形式表示，式（4.8）和（4.9）分别为

显然，动坐标系中某一坐标位置在参考坐标系o′x′y′z′中可表达为

如果（x，y，z）为船体表面上某点的位置坐标，则上式体现了船体摇荡时某一瞬时的空间位置。