船舶在波浪上运动的理论及斯托克斯波的特性

暂且先采用空间固定坐标系o 0x 0y 0z 0。在这个坐标系中，速度势Φ（x 0，y 0，z 0，t），须满足的自由面条件是

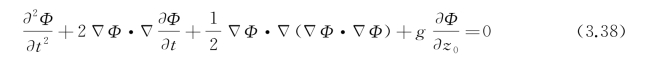
它在自由面z 0=ζ（x 0，y 0，t）上得以满足。自由面方程由下式决定，即

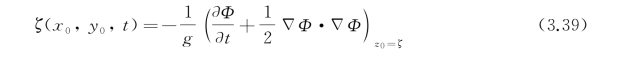
对有限水深H（x 0，y 0），在池底上应满足固壁条件，即

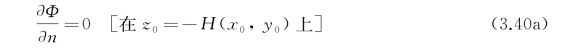
无疑，入射波的速度势ΦI应该满足这组边界条件。不过，若研究底部不平的影响时，一般假定H（x 0，y 0）总是在水平坐标的有限范围内变化，此范围之外，池底是水平的；或者至少在来波侧远方池底是水平的，即水深是均匀的。若记远处水深为H 0（常数），则传来的入射波应在z 0=-H 0上满足条件（3.40a），则式（3.40a）可改写为

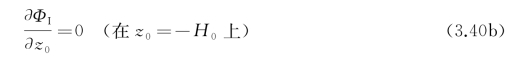
第一个研究无旋有限振幅波在水平河床上传播的是斯托克斯（Stokes）［112］。他利用小参数展开法，该小参数基本上就是波高与波长之比。当时，对无限水深情况，斯托克斯得到了三阶近似；对有限水深情况，得到了二阶近似。1880年，斯托克斯又重新考察了这个问题［113］，采用了与以前不同的方法，对无限水深获得了五阶近似，对有限水深获得了三阶近似。斯托克斯的一阶近似解就是大家熟悉的正弦前进波。正弦波是由艾里（Airy）［114］首先提出的，故又称艾里波，高阶近似就称斯托克斯波。由于这种无旋的前进波在许多工程领域，如海岸工程、离岸工程、船舶流体力学、明渠流动中有着重要的意义，近年来受到各方面的注意。德（De）［115］和斯基伯利及亨德里生（Skjlbeia，Hendrickson）［116］对有限水深计算到5阶，许瓦兹（Schwartz）［117］对有限水深算到48阶，无限水深算到117阶。考克雷（Cokelet）［118］改用不同的小参数，算到110阶。黎奈克（Rienecker）和范登（Fenton）［119］在1981年用数值算法重新计算了这个问题。图3.10是无限水深时的波形图［117］，图中z／λ=0为静水位。

由图3.10可知，斯托克斯波存在着极限波高，其波高波长比是0.141 2，这时波峰呈尖角，尖角的大小如斯托克斯证明的那样为120°。另外，斯托克斯波波峰比较陡峭，波谷比较平坦，但是波峰高出静水面的部分比波谷陷下去的部分多。仅在A／λ较小时，波形才呈余弦状。

斯托克斯波是一个规则的前进波，假设它的前进方向沿正o 0x 0方向，波速为C，波峰与o 0y 0轴平行。显然，这是一个一维的平面前进波，而且，在以波速C移动的坐标系中观察时，波形是定常不变的，即

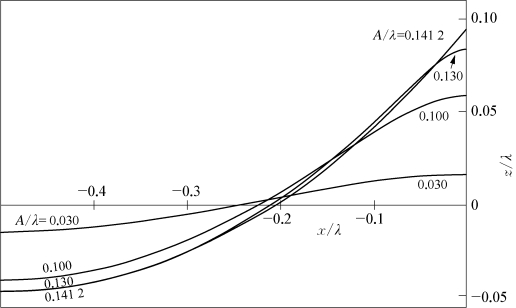
图3.10　无限水深斯托克斯波形

它当然满足拉普拉斯方程。自由面条件式（3.38）和自由面方程式（3.39）经过

变换后，得到在z=ζ（x）上的自由面条件和自由面方程分别为

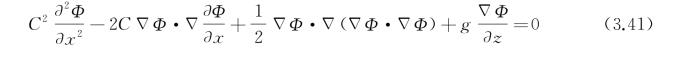
和

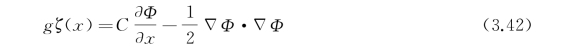
式（3.41）是由自由面上的动力学条件和运动学条件得来的，其动力学条件可表示为

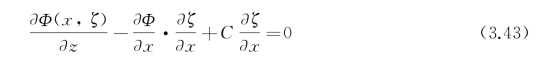
在下面的叙述中，用式（3.42）和式（3.43）代替自由面条件式（3.41）进行讨论。

将变量作摄动展开，即令

在这些级数中，不直接引入小参数，而是认为后项比前项小一个量级。小参数可以是ε=Ak，A为波幅，k为波数。与往常不同的是现在波速C也加以展开，C的展开式中，C（0）是零阶量，以后才是逐次的高阶量。在物理上由于不同阶的近似，对同一波长或波数的波，波速是不同的，如果把波速C作为一个固定的常数，又要从摄动展开中依次得到各阶近似，就无法反映波速在不同阶近似中的变化，在数学处理上就会遇到困难（从三阶以上的近似中开始反映出来）。在方程中把参数加以展开，其实是一种奇异摄动，在非线性振动和天体力学问题中经常遇到［120，121］。将式（3.44）代入式（3.42）和式（3.43），并将Φ及其导数在z=0附近展开，则一阶至三阶近似的自由面条件分别为

各阶速度势Φ（i）（i=1，2，3，…）都满足拉普拉斯方程和池底条件，即

和

这里已假设水深是均匀的，深为H。

第一阶近似是大家所熟知的，即

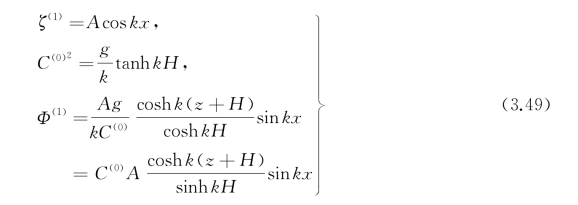
式中，A为波幅。由式（3.49）中第一式可见，一阶近似的波形是余弦型的；波速与波数的关系（色散关系）为式（3.49）中第二式。水深无限时波形不变C（0）2

∞=g／k，Φ（1）

∞=C（0）A e kzsin kx。

将式（3.49）代入式（3.46），经整理可得

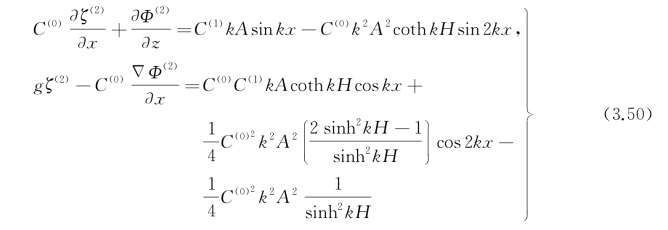
上面两式中右端的第一项分别含sin kx和cos kx。要满足它，势Φ（2）中应含cos k（z+H）／sinh k H·sin kx因子，而它正好是左端等于零的解（对比一阶近似解可知），若令

则上两式中左端第一项同时消失。

先考察H=∞即无限水深的特殊情况，这时coth k H=1，式（3.50）变成

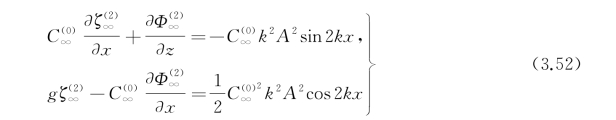
容易看出，若令

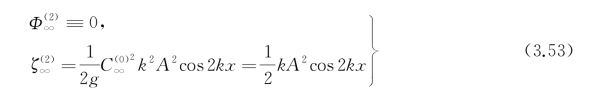
则正好满足式（3.52）。这个结果表明，对于无限水深情况，准确到二阶近似的斯托克斯波是

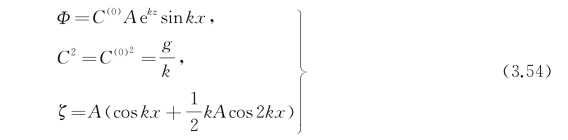
即对深水斯托克斯波来说，通常所用的一阶近似的速度势表达式至少准确到二阶近似，当然，这时波形已经改变了［见式（3.54）中第三式］。

要想得到有限水深的结果，需要回到式（3.50），其中取C（1）=0，并从式（3.50）的两个表达式中消去自由面位移ζ（x），得到

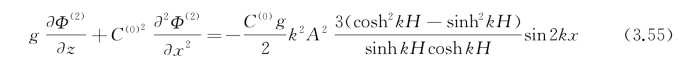
选取解的形式是

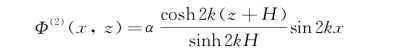
含sin2kx是因为式（3.55）右端因子中含有它，cosh2k（z+H）保证了Φ（2）（x，z）满足拉普拉斯方程和池底条件，sinh 2k H保证了该形式可以光顺地过渡到无限深水的情况。选sinh 2k H而不选cosh 2k H是为了与式（3.49）的形式取得一致，α是待定的，它本身可以是k H的函数，故选sinh2k H或cosh2k H不会影响最后结果。

将上述形式的解代入式（3.55），可证

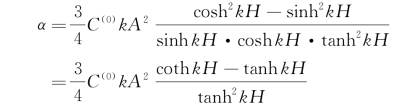
于是二阶速度势Φ（2）为

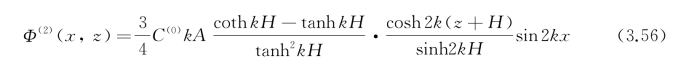
将sinh2k H，coth k H和tanh k H化开，Φ（2）还可以改写成

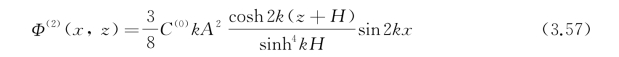
将式（3.56）代入式（3.50）中的第二式，则有

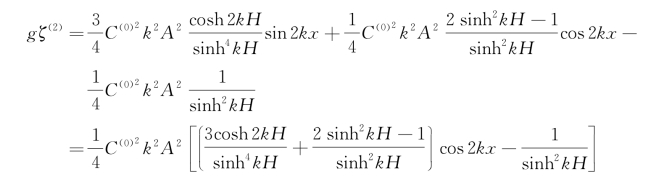
注意到

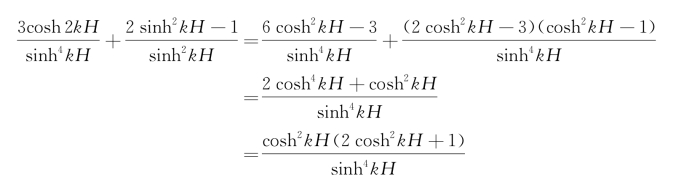
和

于是得到二阶的自由面形状为(www.xing528.com)

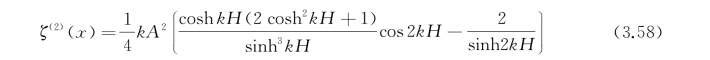
准确到二阶小量，有限水深的斯托克斯波是

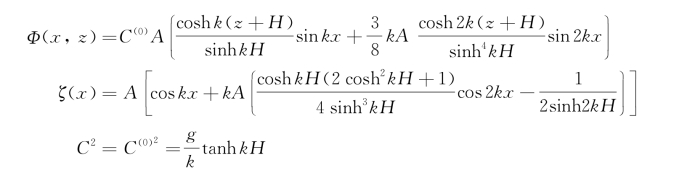
上述结果表明，准确到二阶近似，色散关系不变，波速只取决于波数和水深，与波幅无关。另外，波形的平均位置有所下沉，这个下沉量是k A 2／2sinh 2k H。图3.11是据上述ζ（x）表达式的一个计算例子。为了突出二阶项ζ（2）的影响，k A选的比较大，为0.40，相当于波高波长比0.06，因而造成了波谷反而有点上突。但从总的方面来说，峰尖谷坦的非线性波浪特征都显示出来了。

一个值得注意的谬点是，当k H足够小时，sinh k H→0，从而二阶波浪甚至可能超过一阶的线性项。这自然是不合理的，但它却表明了斯托克斯波浪理论的一种限制，即在k H=2πH／λ足够小的浅水波（H小，λ一定）或长波（H一定，λ大）情况下是不适用的。当k H较小时，sinh3k H≈（k H）3，从二阶波形公式（3.58）中可以看到，斯托克斯波适用的范围是

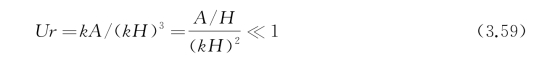
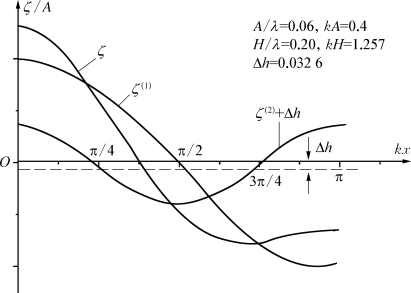
图3.11　ζ（x）的计算例子

即A／H≪4π2（H／λ）2也就是说，波幅与水深之比要远小于水深与波长之比的平方。Ur这个参数是厄塞尔（Ursel1）［122］引进的，称为厄塞尔数。它在浅水波或长波理论中经常会遇到。

目前，关于物体在波浪上运动问题的研究，非线性影响一般最多考虑到二阶，但海洋工程中计算细长杆件的受力时，往往要用斯托克斯五阶波的结果。由于它的推导和表达十分繁杂，我们在此仅推导三阶斯托克斯波。

将前面获得的Φ（1），ζ（1）Φ（2），ζ（2）等代入三阶近似的自由面条件（3.47）中去，经过细致的演算，可得

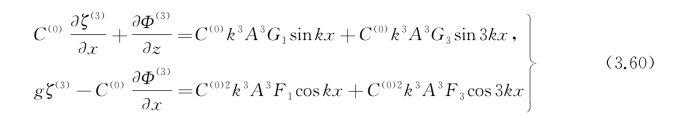
其中

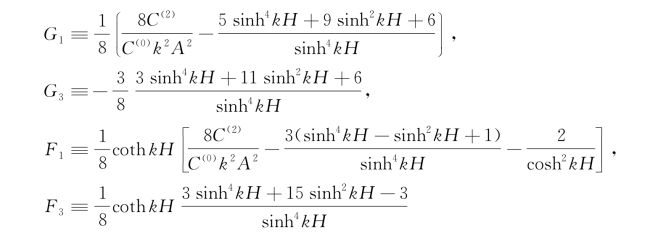
从式（3.60）中消去ζ（3）得到Φ（3）的自由面条件为

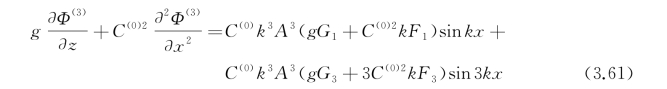
要获得有限的Φ（3），必须使sin kx项的系数等于零。应用一阶近似的色散关系C（0）2k=g tanh k H，可以得到

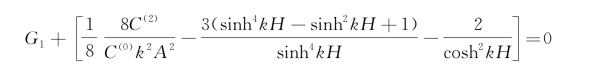
从中可解出

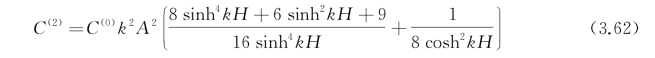
于是包含三阶近似的色散关系是

上式表明，波速不仅取决于水深和波数，还与波幅或波倾角有关，这是非线性波的一个重要特点，但要准确到三阶近似中才显露出来，关于无限水深对应的色散关系退化为［123］

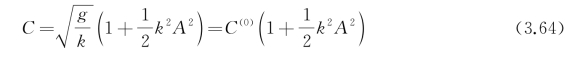
选取Φ（3）的形式为

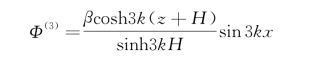
将其代入式（3.61），可得

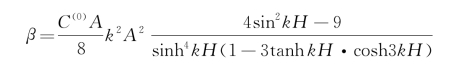
所以

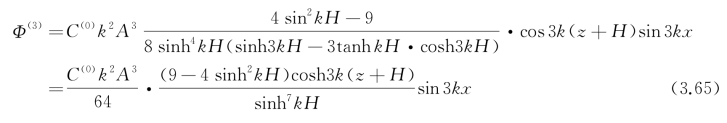
其中已应用了双曲函数的简单的变换关系：

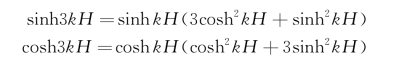
将得到的Φ（3）代入式（3.60）中第二式，得到

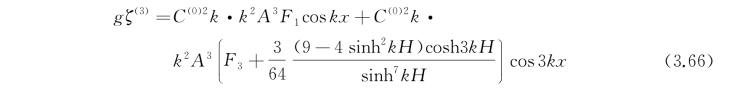
其中F 1中的C（2）按式（3.62）代入，整理后有

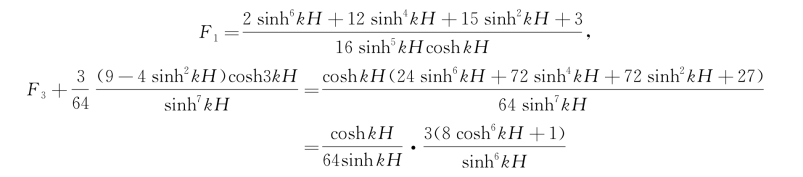
将它们代入式（3.66），并应用关系，最后可得

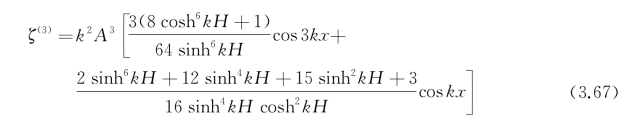
三阶自由面不仅含有cos3kx项，而且含有cos kx项，后者与线性项同相，周期也相同，只是幅度小k 2A 2倍。作为特例，考察H→∞的极限情况。由式（3.63）和式（3.67）有

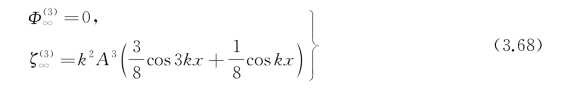
这是一个非常有趣的结果，对无限水深而言，准确到三阶小量，势函数仍可用线性结果表示，即

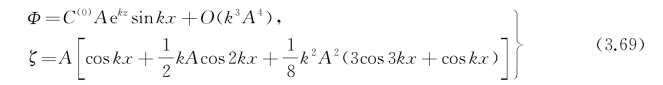
对应的流体质点的速度（绝对速度）是

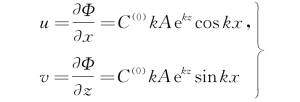
对同一个x=x 0-Ct，流体质点速度随水深的增加按指数衰减，而且对0＜z≤ζ也同样适用，这里ζ为自由面垂向位置坐标。特别是在波峰kx=0处和波谷kx=π处，流体质点的垂向速度为零，在同一深度z上水平速度绝对值是一样的，唯波峰处水平速度向前，波谷处水平速度向后，准确到三阶小量，流场中各点的压强可按下式计算：

式（3.70）由拉格朗日积分导出，其中积分常数由波面上p 0=0决定。

在用高阶理论计算流体质点的轨迹时，出现一个特别有趣的现象，称为质量传输。质点的运动方程为

鉴于Φ（x 0-Ct，z 0）是小参数ε（例如ε=k A）的函数，解x 0和z 0也将依赖于小参数ε。将它们展开：

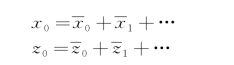
并代入式（3.71），再对∂Φ（x 0-Ct，z 0）应用适当的展开式，得到一系列的方程式，其中前二阶表达式为

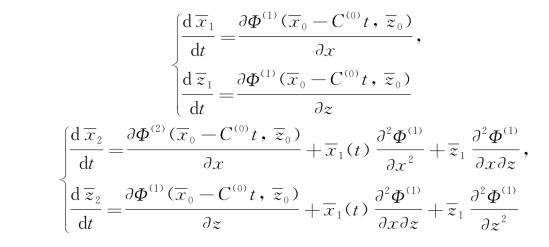
对无限深水情况，Φ（2）≡0。一阶解是熟知的（见3.3节），即

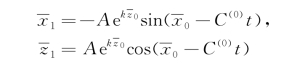
即流体质点偏离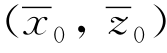）作圆周运动。二阶量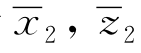满足方程：

其解是，准确到二阶小量的质点运动轨迹：

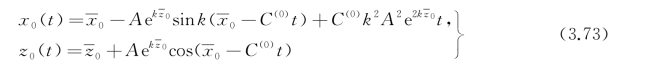
项C（0）k 2A 2e2kz0t的存在表明流体质点除了作轨圆运动外，还有一个持续不断的水平漂移。这个移动破坏了质点在一阶理论中的圆形轨迹，移动速度的大小随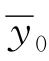按指数减小。对任一垂直于波向的截面，将式（3.72）沿（-∞，ζ）对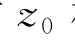积分，准确到二阶小量，得到流量的传输为

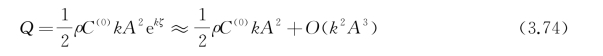
考虑到有限水深H的影响，同样准确到二阶小量，流体质点的运动轨迹［124］：

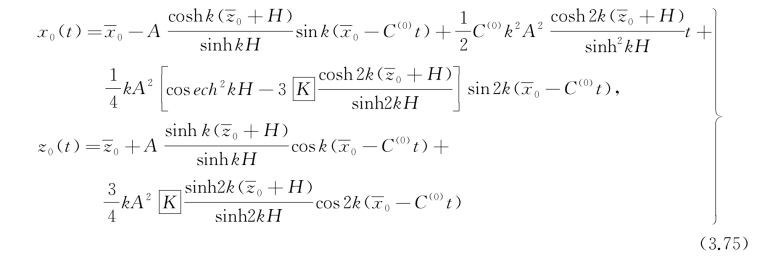
式中，

上式表明x方向的质量传输依然存在，而且蔓延到整个水深H的范围内。流体质点除了水平漂移之外，还附加了一个波长减半，频率加倍的周期性运动。